8.__________________________ Concentrator Optics
To this point, we have developed an understanding of how solar energy is collected by flat-plate collectors…those where the entire area that the sun’s radiation falls, absorbs the incident energy. Concentrating collectors, on the other hand, use large reflectors to ´concentrate´ the incident solar energy onto a smaller receiver. The main goal for doing this is to increase the temperature of the heat collected from the sun. Increased temperature is a benefit for many industrial process uses, and is directly connected to the efficiency at which electricity can be produced from thermal sources.
In the following sections we will develop the analytical tools necessary to understand the basic concepts of concentration of solar energy, in parabolic trough, parabolic dish, central receivers and Fresnel lens solar collection systems. These tools will be presented with the following outline:
Concentration Ratio
The Parabola
Parabolic Cylinder
Paraboloid
Parabolic and Spherical Optics
Two-dimensional Ray Trace Diagrams
Line-focus Troughs
Point-focus Dishes
Reflection of Energy to the Receiver
Reflection of Parallel Rays
Reflection of Non-parallel Rays
Contribution of Errors
Principles of Reflection and Refraction
Mirrors
Lenses
Total Internal Reflection
Dielectric Reflection and Antireflection Coatings
The operation of any solar thermal energy collector can be described as an energy balance between the solar energy absorbed by the collector and the thermal energy removed or lost from the collector. If no alternative mechanism is provided for removal of thermal energy, the collector receiver heat loss must equal the absorbed solar energy.
The temperature of the receiver increases until the convective and radiation heat loss from the receiver equals the absorbed solar energy. The temperature at which this occurs is termed the collector stagnation temperature.
For control of the collector temperature at some point cooler than the stagnation temperature, active removal of heat must be employed. This heat is then available for use in a solar energy system. The rate at which heat is actively removed from the collector determines the collector operating temperature. For removal of a large fraction of the absorbed solar energy as useful heat, the amount of heat lost from the receiver must be kept small.
Receiver heat loss can be reduced by operating the collector near the ambient temperature (such as with low-temperature flat-plate collectors) or by constructing the collector such that heat loss at elevated temperature is reduced. The most common way of reducing receiver heat loss at elevated temperatures is to reduce the size of the hot surface (i.e., the receiver) since heat loss is directly proportional to area of the hot surface. Concentrating collectors reduce the area of the receiver by reflecting (or refracting) the light incident on a large area (the collector aperture) onto an absorber of small area. With reduced heat loss, concentrating collectors can operate at elevated temperatures and still provide significant quantities of useful thermal energy.
A second reason for using concentration in the design of solar collectors is that, in general, reflective surfaces are usually less expensive than absorbing (receiver) surfaces. Therefore, large amounts of inexpensive reflecting surface area can placed in a field, concentrating the incident solar energy on smaller absorbing surfaces. However, concentrating collectors must track the sun´s movement across the sky, adding significant cost to the construction of a concentrating collector system.
8.1.1 Concentration Ratio
The term "concentration ratio" is used to describe the amount of light energy concentration achieved by a given collector. Two different definitions of concentration ratio are in general use. They are defined briefly here so that the terms may be used.
Optical Concentration Ratio (CRo). The averaged irradiance (radiant flux) (
Ir ) integrated over the receiver area (Ar), divided by the insolation incident on the collector aperture.Geometric Concentration Ratio (CRg). The area of the collector aperture Aa divided by the surface area of the receiver
ArOptical concentration ratio relates directly to lens or reflector quality; however, in many collectors the surface area of the receiver is larger than the concentrated solar image.
Thermal losses in such situations are larger than might be inferred from examination of the optical concentration ratio. Since geometric concentration ratio refers to receiver area, it is most commonly used because it can be related to collector heat loss [e.g., see Chapter 5] . Note that if the aperture insolation and receiver irradiance are both uniform over the entire area, the optical and geometric concentration ratios are equal.
Perhaps the simplest solar concentrator is a concentrating flat-plate collector. An example of such a collector is shown in Figure 8.1. This type of concentrator is a flat-plate collector surrounded by mirrors that reflect sunlight incident outside the normal perimeter of the flat plate onto the absorber plate of the collector. This type of collector is usually constructed to reduce the cost of a flat-plate collector by reducing the area of the absorber and cover plates, which are frequently expensive. A concentrating flat-plate collector such as that shown in Figure 8.1 is typically limited to geometric and optical concentration ratios of 2-3.
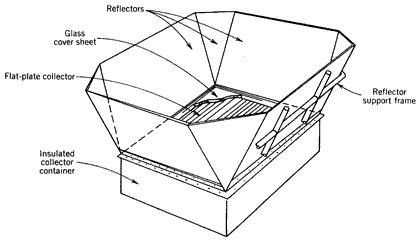
Figure 8.1
A concentrating flat-plate collectorIf higher concentration ratios are desired, curved mirrors or lenses are used. Circular and parabolic mirror optics are described in Section 8.3, and Fresnel lenses are examined in Section 8.7.
8.2.1 The Parabola
A parabola is the locus of a point that moves so that its distances from a fixed line and a fixed point are equal. This is shown on Figure 8.2, where the fixed line is called the directrix and the fixed point
F, the focus. Note that the length FR equals the length RD. The line perpendicular to the directrix and passing through the focus F is called the axis of the parabola. The parabola intersects its axis at a point V called the vertex, which is exactly midway between the focus and the directrix.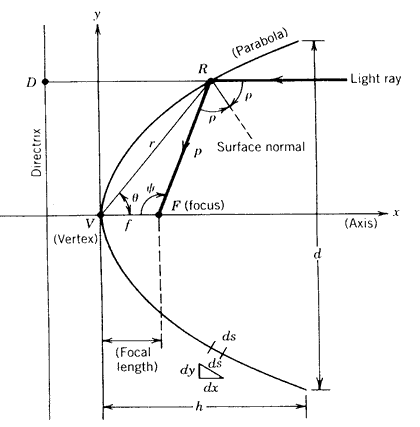
Figure 8.2
The parabola.If the origin is taken at the vertex
V and the x-axis along the axis of the parabola, the equation of the parabola is
(m2) (8.3)
where f, the focal length, is the distance VF from the vertex to the focus. When the origin is shifted to the focus F as is often done in optical studies, with the vertex to the left of the origin, the equation of a parabola becomes
(m2)
(8.4)
In polar coordinates, using the usual definition of r as the distance from the origin and the angle from the x-axis to r, we have for a parabola with its vertex at the origin and symmetrical about the x-axis
(8.5)
Often in solar studies, it is more useful to define the parabolic curve with the origin at F and in terms of the angle in polar coordinates with the origin at F . The angle
is measured from the line VF and the parabolic radius p, is the distance from the focus F to the curve. Shifting the origin to the focus F, we have
(m)
(8.6)
The parabolic shape is widely used as the reflecting surface for concentrating solar collectors because it has the property that, for any line parallel to the axis of the parabola, the angle p between it and the surface normal is equal to the angle between the normal and a line to the focal point. Since solar radiation arrives at the earth in essentially parallel rays and by Snell's law the angle of reflection equals the angle of incidence, all radiation parallel to the axis of the parabola will be reflected to a single point F, which is the focus. Careful inspection of the geometry described in Figure 8.2 will show that the following is true:
(8.7)
The general expressions given so far for the parabola define a curve infinite in extent. Solar concentrators use a truncated portion of this curve. The extent of this truncation is usually defined in terms of the rim angle or the ratio of the focal length to aperture diameter f/d. The scale (size) of the curve is then specified in terms of a linear dimension such as the aperture diameter d or the focal length f. This is readily apparent in Figure 8.3, which shows various finite parabola having a common focus and the same aperture diameter.
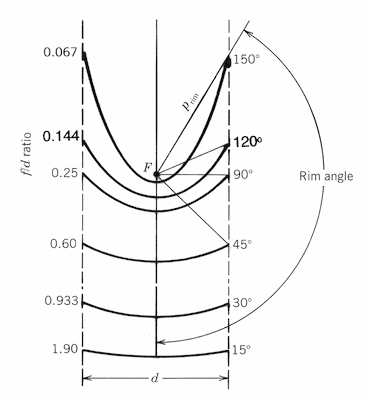
Figure 8.3
Segments of a parabola having a common focus F and the same aperture diameter.It can be seen that a parabola with a small rim angle is relatively flat and the focal length is long compared to its aperture diameter. Once a specific portion of the parabolic curve has been selected, the height of the curve,
h may be defined as the maximum distance from the vertex to a line drawn across the aperture of the parabola. In terms of focal length and aperture diameter, the height of the parabola is
(8.8)
In a like manner, the rim angle may be found in terms of the parabola dimensions:
(8.9)
Another property of the parabola that may be of use in understanding solar concentrator design is the arc length s. This may be found for a particular parabola from Equation (8.3) by integrating a differential segment of this curve and applying the limits x = h and y = d/2 as pictured in Figure 8.2. The result is
(8.10)
where d is the distance across the aperture (or opening) of the parabola as shown in Figure 8.2 and h is the distance from the vertex to the aperture. The cross sectional area of the space enclosed between a parabola and a line across its aperture and normal to the axis is given by
(8.11)
this area should not be confused with the reflecting surface area of a parabolic trough or dish or their aperture areas, the equations for which are given in the following section.
Often in evaluating parabolic geometry and related optical derivations, the casual reader becomes confused with the many forms used to represent the geometry of a particular parabolic shape. The following equivalencies are given for the convenience of the reader:
(8.12)
(8.13)
(8.14)
(8.15)
8.2.2 Parabolic Cylinder
The surface formed by moving a parabola along the axis normal to its plane is called a parabolic cylinder. Solar concentrators with this type of reflecting surface are often called parabolic troughs because of their appearance, or line focus concentrators because the foci of the parabola describe a line in this geometry. When the plane containing the axes of the parabola is aligned parallel to the rays of the sun, the rays are focused on this focal line. For a parabolic cylinder of length l and having the cross-sectional dimensions shown in Figure 8.2, the collector aperture area is given by
(8.16)
The reflective surface area is found by using the arc length developed in Equation (8.10):
(8.17)
The focal length f and the rim angle for the parabolic cylinder are given in Equations (8.8) and (8.9).
8.2.3 Paraboloid
The surface formed by rotating a parabolic curve about its axis is called a paraboloid of revolution. Solar concentrators having a reflective surface in this shape are often called parabolic dish concentrators. The equation for the paraboloid of revolution as shown in Figure 8.4, in rectangular coordinates with the z-axis as the axis of symmetry, is
(8.18)
where the distance f is the focal length VF. In cylindrical coordinates, where a is the distance from the z-axis, this becomes
(8.19)
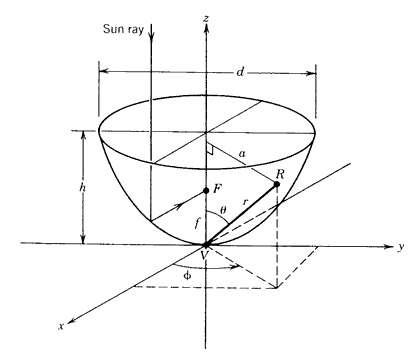
Figure 8.4
Paraboloid of revolution.In spherical coordinates, the equation of a paraboloid of revolution with its vertex
V at the origin and r,The surface area of the paraboloid may be found by integrating Equation (8.19) over the appropriate limits. We can define a circular differential area strip on the paraboloid as shown in Figure 8.5 as
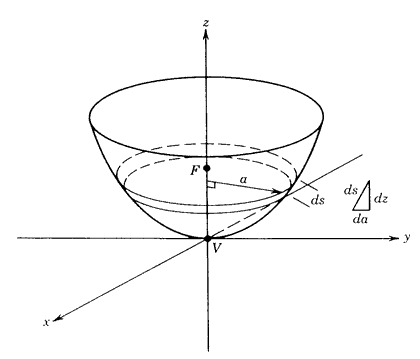
Figure 8.5
Parameters defining a circular strip of differential area.Note that the differential element of arc
ds is cast in terms of the height dz and the radial distance da. Finding the derivative of z with respect to a using Equation (8.19), we express the differential area band as
(8.22)
The full surface area A, of a paraboloid having a focal length f and an aperture diameter d may be found by integrating Equation (8.22). The result is
(8.23)
The concentrator aperture area, of most importance to the solar designer for
prediction of solar concentrator performance, is simply the circular area defined by the aperture diameter d and is given by
(8.24)
An equation for the aperture area may also be cast in terms of the focal length and the rim angle. Using Equation (8.6), which is the polar form of the equation of a parabola, we have
(8.25)
Note: Equation (8.26) has been renumbered and moved to another chapter. (8.26)
8.3 Parabolic and Spherical Optics
Both spherical and parabolic geometries are represented in solar thermal concentrators. In some concentrators, however, a spherical (or more usually cylindrical) geometry is used as an approximation to a true parabola. As will be shown in Chapter 9, spherical optics allow for fixed- aperture (i.e., non-tracking) concentrators. Since parabolic geometries strongly dominate solar concentrators, a rather thorough examination of the analytical description of parabolic geometry is presented in this chapter.
In order to facilitate a discussion of spherical and parabolic optics, it is convenient to define the term ‘plane of curvature’, as illustrated for a parabolic trough in Figure 8.6.
The plane of curvature (i.e., cross section) can be considered as a two-dimensional slice normal, in the case of a parabolic trough, to the linear axis of the concentrator. For a spherical or a parabolic dish, the plane of curvature is rotated to generate the dish geometry. The optical principles of spherical and parabolic mirrors are examined below through ray trace diagrams and by initially restricting the discussion to the plane of curvature. The impact of translation or rotation of the plane of curvature is then discussed in order to evaluate the optical characteristics of actual concentrator geometries.
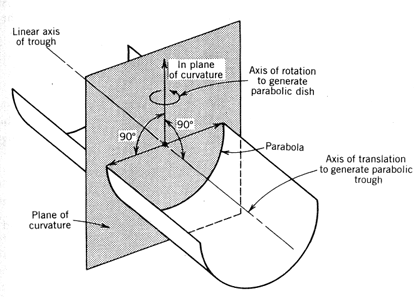
Figure 8.6
Definition of plane of curvatureThe purpose of a general discussion at this point, prior to examining individual concentrator concepts, is to develop an understanding of the basic limitations imposed by spherical and parabolic geometries and how these limitations impact basic concentrator design.
The equation of a circle as drawn in Figure 8.7a in Cartesian coordinates with its center at
a, b and radius r is
which reduces to the familiar form
when the circle is centered at (
0,0). The equation for a line tangent to this circle at the point (x1 , y1) is
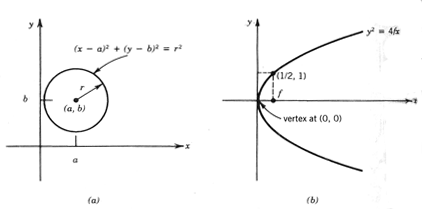
Figure 8.7 Definition of (a) circle and (b) parabola
A parabola (see Figure 8.7b) can be defined as any section of a right circular cone resulting from a plane slicing through the cone parallel to, but not including, the axis of the cone. The equation for a parabola, with focal length f, in the Cartesian coordinates is
(8.30)
The vertex of a parabola having this form will be at (0,0). The equation of the tangent to this parabola at (x1 , y1) is
(8.31)
These basic equations are useful in examination of the optical properties of spherical and parabolic mirrors.
Another characteristic useful in discussing parabolic or spherical mirrors is the rim angle. Rim angle is defined graphically in Figure 8.8 for a parabolic trough. A similar definition holds for parabolic dishes and mirrors based on spherical geometry.
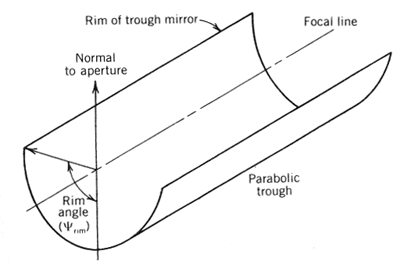
Figure 8.8
Definition of rim angle8.3.1 Two -Dimensional Ray Trace Diagrams
The reflections of parallel rays of sunlight from both two dimensional circular and parabolic mirrors are shown in the ray trace diagrams in Figures 8.9 and 8.10, respectively. The characteristics of these two mirrors in concentrating parallel rays of incident light which are normal to the reflector aperture are:
2. All parallel rays reflected from a parabolic mirror, when they are parallel to the axis of symmetry, intersect at a point (see Figure 8.10a).
In addition, a circular mirror is symmetrical with respect to rotations about its center. This means that if the sun’s rays (assumed to be parallel for this discussion) are not normal to the mirror’s aperture as in Figure 8.9a, the pattern of reflected rays looks the same but is rotated (see Figures 8.9b and 8.9c).
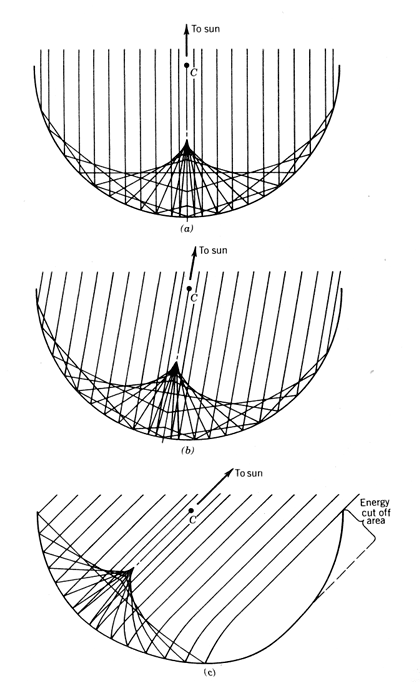
Figure 8.9
Characteristics of spherical optics (C = center of circle).A parabolic mirror, on the other hand, is not symmetrical to rotations about its focal point. As shown in Figure 8.10, if the incident beam of parallel rays is even slightly off normal to the mirror aperture, beam dispersion occurs, resulting in spreading of the image at the focal point. For a parabolic mirror to focus sharply, therefore, it must accurately track the motion of the sun to keep the axis (or plane) of symmetry parallel to the incident rays of the sun.
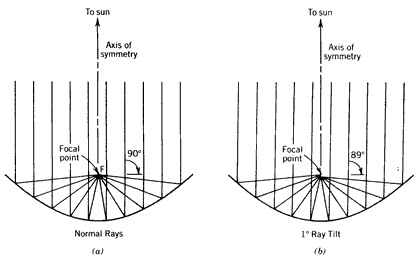
Figure 8.10 Characteristics of parabolic optics, (a) for rays parallel to the axis of symmetry, (b) for rays 1o off of the axis of symmetry.
8.3.2 Line Focus Troughs
To form either a cylindrical or parabolic trough, the two-dimensional mirrors shown in Figures 8.9 and 8.10 must be translated normal to the plane of curvature as illustrated in Figure 8.11. Tracking requirements of the linear troughs are similar to that of the two-dimensional mirrors discussed above.
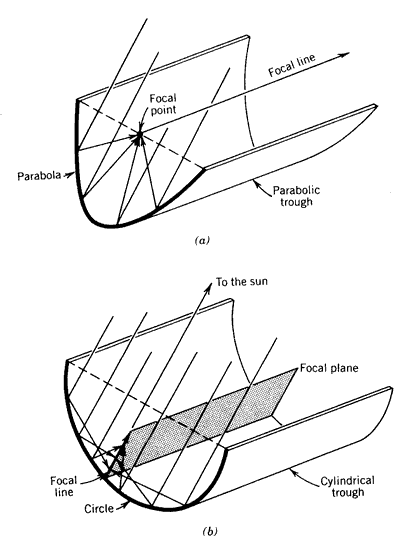
Figure 8.11
Formation of linear troughs: (a) parabolic trough; (b) cylindrical trough.A parabolic trough as shown in Figure 8.11a has a line focus and must be tracked about its linear axis in order to maintain focus. The proper tracking angle is defined by the orientation of the trough relative to the sun’s position. Analytical expressions for the proper tracking angle of parabolic troughs are developed in Chapter 4. Basically, a parabolic trough must track about its linear axis so that when the sun’s rays are projected onto the plane of curvature, they are normal to the trough aperture.
Since linear translation does not introduce curvature along the translation axis, the trough need not be tracked in this direction in order to maintain focus. Just as reflection from a plane mirror does not defocus parallel rays of light, neither is the component of the incident beam (direct) insolation in the plane of translation defocused by a linear translation. The net effect of a non-normal incidence angle
Figure 8.12 shows a photograph of a receiver tube illuminated by direct insolation entering the trough aperture with a non-normal incidence angle. In this case, the trough has been tracked about its linear axis as indicated by the highly focused beam image on the receiver tube. As a result of the non-normal incidence angle, however, the reflected beam is translated down the receiver tube; note that the right end of the receiver tube is dark. At the far end of the parabolic trough some of the incident insolation is reflected past the end of the receiver tube. This is illustrated in Figure 8.13 for another collector. Note that some concentrated light is failing on the flexible hose and not on the receiver. This energy is lost to the collector and is called the collector endloss.

Figure 8.12 Translation of focused radiation along receiver tube due to non-normal incident insolation.
Courtesy of Sandia National Laboratories.
Figure 8.13
Parabolic trough endloss. Courtesy of Sandia National Laboratories.Since linear translation does not introduce defocusing of the concentrated radiation, the aperture of a cylindrical trough need not track at all to maintain focus. However, as indicated in Figure 8.11b, a high-rim angle cylindrical trough would have a focal plane not a focal line. To avoid a dispersed focus, cylindrical troughs would have to be designed with low rim angles in order to provide an approximate line focus. The advantage of a cylindrical mirror geometry is that it need not track the sun in any direction as long as some means is provided to intercept the moving focus.
The effect of rim angle
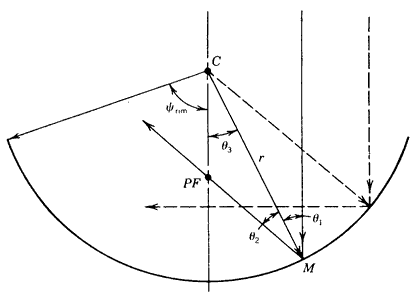
Figure 8.14 Definitions of angles for reflection from a cylindrical (or spherical) mirror.
Point
PF is termed the paraxial focus. AsFor practical applications, if the rim angle of a cylindrical trough is kept low (e.g., <20-30 degrees ), spherical aberration is small and a virtual line focus trough is achieved. Figure 8.15 shows the focusing of circular mirrors with various rim angles.
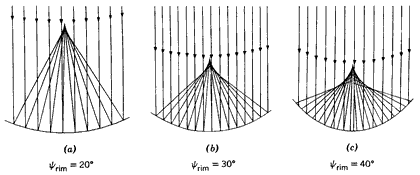
Figure 8.15 Focusing of parallel rays of light using circular mirrors with different rim angles.
8.3.3 Point Focus Dishes
If the two-dimensional curved mirrors shown in Figures 8.9 and 8.10 are rotated rather than translated, the resulting geometric figures are spherical and parabolic dishes, respectively. A parabolic dish must be tracked in two dimensions in order to maintain the incident beam insolation normal to the dish aperture at all times to allow focusing. As with the cylindrical trough, however, the aperture of a spherical dish need not be tracked because of the symmetry of a sphere (circle) as discussed earlier. However, a linear receiver that tracks the moving focal line (see Figure 8.9) must be provided. A prototype parabolic dish concentrator is described in Chapter 9 along with a prototype non-tracking aperture spherical dish.
8.4 Reflection of Energy to the Receiver
Although the design details of any one parabolic collector may differ from those of another parabolic collector, optical constraints define the basic configuration of all parabolic concentrators. This section reviews these constraints and examines the process of supplying concentrated optical energy to the receiver. Heat-loss considerations are addressed in Section 9.2. The basic logic flow followed in this review is summarized in Figure 8.16. The reflection of parallel rays of light, normal to the collector aperture, is reviewed. The goal is to develop an analytical equation that shows the contribution of light reflected to the focus as a function of rim angle.
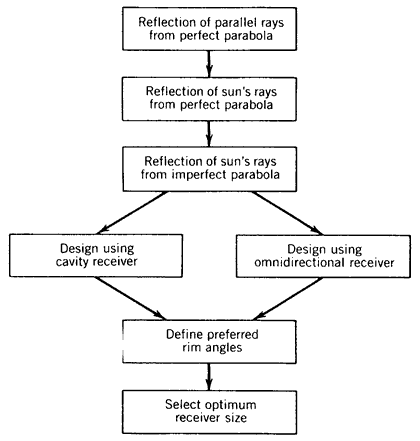
Figure 8.16
Optical analysis of parabolic concentrators.This analysis is then modified to account for the fact that the sun’s rays are not truly parallel. Angular errors (e.g., slope errors) in the conformity of the reflector surface to a true parabolic shape are incorporated at this stage. The spread of the reflected beam due to errors in mirror surface slope, tracking, and nonparallel solar rays provides the information needed to examine the principles used in selecting the size of the receiver.
An examination of the resulting concentration ratios yields information about the approximate rim angle for a parabolic collector. Heat-loss considerations discussed in Section 9.2 will further constrain the design of the receiver.
8.4.1 Reflection of Parallel Rays
Consider the parabolic mirror illustrated in Figure 8.17. A ray of light, with intensity of
Ib incident parallel to the axis of the parabola, will be, as shown, reflected to the focus F of the parabola. Since we will want to discuss the total quantity of light reflected by the entire mirror surface, it is convenient to first consider a differential area
(8.32)
where
ds = differential arc length of the parabola shown in Figure 8.17
l = either length of a differential strip on the surface of a parabolic trough along the direction of the focal line, or circumference of the differential ring on the surface of a parabolic dish.
An expanded view of Figure 8.17a shows the angles associated with
ds.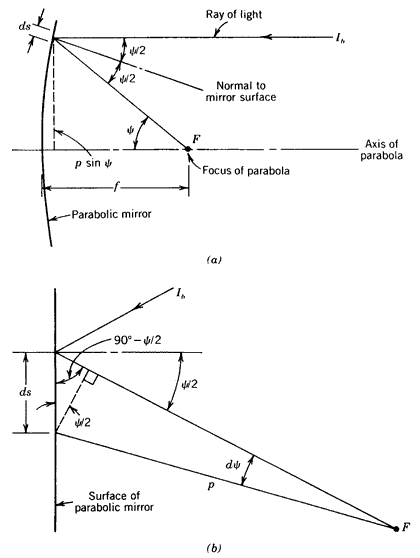
Figure 8.17
Reflection of a light ray from a parabolic mirror.Application of Figure 8.17b yields
(8.33)
Since the angle is small,
, and Equation (8.33) reduces to
(8.34)
Thus
(8.35)
The total radiant flux reflected from this differential area (assuming no reflectance loss) to the point of focus is
(8.36)
Substitution of equation 8.6 for p (see Section 8.2) results in
(8.37)
Equation (8.37) is the general form of the equation and holds for both parabolic troughs and dishes. However, for a parabolic dish we can substitute for l in Equation (8.37). Introducing the subscripts PT and PD to signify parabolic trough and parabolic dish, respectively, we can rewrite Equation (8.37) as
(8.38a)
and
(8.38b)
where the following substitution was used (see Figure 8.17).
(8.39)
8.4.2 Reflection of Nonparallel Rays
The preceding discussion is based on the incident light rays being parallel. This is not true for solar applications. Because of the finite angular size of the sun’s disc (about 33 minutes of arc or 9.6 mrad), the sun’s rays reaching the concentrator are not parallel. Thus, rather than all the incident rays being reflected to the focal point (or line in the case of a trough), the reflected rays form an "image" of finite size centered about the focus. The geometry involved is illustrated in Figure 8.18, where the angular size of the sun’s disc is denoted by .
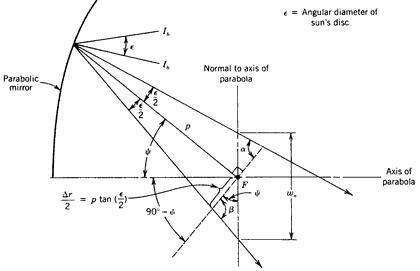
Figure 8.18
Reflection of nonparallel rays from a parabolic mirror.The width (beam spread) of the reflected sun’s image
(8.40)
This is the minimum beam spread that will occur. Any errors in, for example, the trueness of the mirror slope will cause additional spreading of the image size.
8.4.3 The Contribution of Errors
In addition to the finite angular size of the sun, independent errors in the conformity of the mirror to a true parabolic shape (i.e., slope errors), non-specular reflection of the incident light beam, tracking errors, and receiver alignment errors all contribute to further apparent spreading of the reflected light beam. Typically, these errors are assumed to be random and are reported in standard deviation units. Their combined effect is statistically determined. Although the sun’s intensity is not normally distributed across its disc, it may be approximated as a standard distribution so that it can be treated similarly to the concentrator errors.
Harris and Duff (198l) have evaluated the use of a normal distribution to describe the sun’s intensity. They found that the approximation does not introduce significant errors for parabolic troughs and dishes. Table 8.1 shows a typical list of concentrator errors along with the equivalent width of the sun. These errors are for one standard distribution unit , which means that approximately 68 percent of all measurements of the errors fall within the angular deviations noted.
Table 8.l Typical Parabolic Concentrator Errors
|
Type and Source |
Effective |
|
One-Dimensional
|
Structure |
2.5 mrad × 2 = 5 mrad |
25 |
|
Tracking: |
||
|
Sensor |
2 mrad |
4 |
|
Drive Non-uniformity |
2 mrad |
4 |
|
Receiver: |
||
|
Alignment, etc. |
2 mrad |
4 |
|
|
||
|
|
Two-Dimensional
|
Mirror specular reflectance |
0.25 mrad × 2 = 0.50 mrad |
0.25 |
|
Sun 's width |
2.8 mrad |
7.84 |
|
|
||
|
|
||
Total Effective Error
|
|
Note that the
Note also that Table 8.1 is divided into two main parts: one-dimensional errors, and two-dimensional errors. One-dimensional errors are those errors that contribute to beam spreading in the plane of curvature. They are combined as
(8.41)
Note that the slope error is multiplied by 2. This is a result of Snell’s law (Equation 8.54) and the fact that with a slope error, the mirror surface direction is changed whereas the receiver position is not (see Figure 8.19).
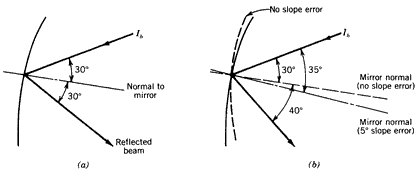
Figure 8.19
Impact of slope error on beam deflection.Figure 8.19a shows the reflection of the beam with no slope error. If, as illustrated in Figure 8.19b, there is a slope error of 5 degrees, the reflected beam is misdirected by an amount of 10 degrees from the original reflected path. In the case of a tracking error, for example, the receiver moves together with the mirror surface so that the factor of 2 does not appear for this type of error in Equation (8.41). The factor of 2 appears only when an error is the result of a movement on the mirror surface and not the receiver.
Two-dimensional errors
(8.42)
where is the solar angle of incidence. The total
error is then
(8.43)
Note that at normal incidence . For a parabolic dish therefore,
is always equal to 0. Incorporation of these error considerations into the above equation for Δr is accomplished by replacing
with some multiple of
. Equation (8.40) can then be rewritten as
(8.44)
where n is the number of standard deviations being considered.
One can expect 68 percent of the energy incident on that part of the reflecting surface (defined by p) to fall on line Δr when n is chosen to be equal to 2 (i.e. ). It is common to use ±
2 to ±
3 times
in solar analyses to ensure that 95 percent or more of all possible energy is captured.
Table 8.2. Percent of Measurements of Flux Falling
Within Multiples of a Given Standard Deviation
|
Multiples of Standard |
Percent |
|
|
Deviation |
n |
Within Limits |
|
±l |
2 |
68.27 % |
|
±2 |
4 |
95.45 % |
|
±3 |
6 |
99.73 % |
8.5 Reflection to a Fixed Point (the Power Tower)
With central receiver systems, the sun 's rays that hit a field of movable mirrors (heliostats) are reflected to a single fixed point in space (the receiver). The tracking angles for the reflector surface, along with the angle of incidence to this surface, may be derived using the vector techniques developed in Chapter 4.
The appropriate geometry can be best described by using zenith, east, and north (z, e, n) coordinates with their origin O at the base of the aim point A
as shown in Figure 8.20. The location of a reflecting surface B can be defined as z1, e1 and n1 and the aim point located at a distance z0 above the origin.
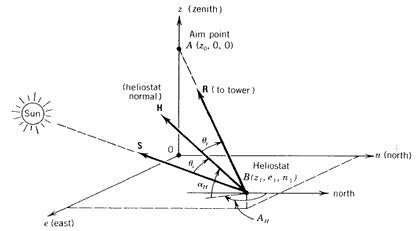
Figure 8.20 Coordinates defining the reflection of the sun’s rays by a heliostat to a single aim point. Vector H is normal to the heliostat reflecting surface
To predict the reflector (heliostat) altitude
where
i, j, and k are unit vectors in the z, e, and n directions, respectively. Defining Equation (8.45) in terms of direction cosines, we haveThe third vector of interest is a unit vector normal to the reflector surface. This is defined as
(8.47)
Table 8.3 summarizes the sign conventions used to develop the angles related to heliostat design.
Table 8.3 Sign Convention for Important Heliostat Angles
|
Title |
Symbol |
Zero |
Positive Direction |
Range |
Equation No. |
Figure No. |
|
Heliostat Angles |
||||||
|
Angle of Incidence |
|
perpendicular to surface |
toward surface |
0 to 90o |
8.49 |
8.20 |
|
Surface Altitude |
|
horizontal |
up |
0 to 90o |
8.51 |
8.20 |
|
Surface Azimuth |
AH |
due north |
clockwise |
0 to 360o |
8.52 or 8.53 |
8.20 |
Since the laws of specular reflection require that the angle of incidence is equal to the angle of reflection, an expression for this angle can be written in terms of the central sun ray unit vector (S) and the aim point unit vector (R) as
(8.48)
Using Equations (3.9) and (8.46), we have
(8.49)
from which the angle of incidence or reflection can be obtained, if we know the position of the sun and the position of the aim point relative to the reflection surface.
The reflection surface unit normal (H) can be found by adding the incidence and reflection vector and dividing by the appropriate scalar quantity. This gives
(8.50)
Substituting Equation (3.9) and describing the altitude and azimuth of the reflecting surface and (AH ) respectively, in terms of the orthogonal coordinates in a manner similar to that shown in Figure 3.6, we have
(8.51)
and
(8.52)
The third expression is redundant but is written here for completeness:
(8.53)
When the reflector azimuth is found by using the arc sine and arc cosine functions, the problem of quadrant ambiguity must again be recognized. It could be handled analytically by solving both Equations (3.52) and (3 .53) or with simpler logic i.e. it is obvious that the angle of incidence cannot exceed 90 degrees.
EXAMPLE: As an example of the use of these equations, take the case where the aim point
A (receiver) is 200 m above a reflector (heliostat) that is located 100 m east and 50 m north of the base of the tower. If the solar altitude angle is 50 degrees with a solar azimuth of 180 degrees, solutions of Equations (8.49), (8.51), and (8.52) give an angle of incidence8.6 Principles of Reflection and Refraction
The basic processes that take place when light encounters the surface of a transparent material are shown in Figure 8.21. A portion of the incident ray may be reflected from the surface as shown, with an angle equal to the angle
where the symbols are defined as in Figure 8.21.
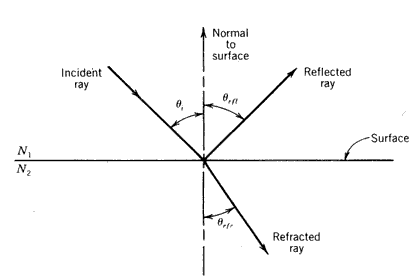
Figure 8.21
Interaction of light with a material. N1, index of refraction of material 1; N2, index of refraction material 2.As the light passes through the material, some of it may be absorbed, thus decreasing the energy content of the refracted light. The ability of material to pass light is reported as transmittance
8.6.1 Mirrors
All reflector surfaces follow the basic principle shown in Figure 8.21, specifically, that the angle of incidence
Specular Reflectance
Non-specular Reflectance The fraction of incident light energy that is reflected from a surface such that the angle
of the reflected beam is not defined by the angle
that the incoming beam makes with the normal to the average surface contour.
Specular reflectance is normally reported for specific acceptance angles through which the measuring instrument will allow light to pass. Figure 8.22 illustrates the measurement of specular reflectance. Analytically, this relationship can be written as
(8.55)
where Ir,a is the reflected irradiance falling within the acceptance angle and Ib
is the irradiance of the incident beam.
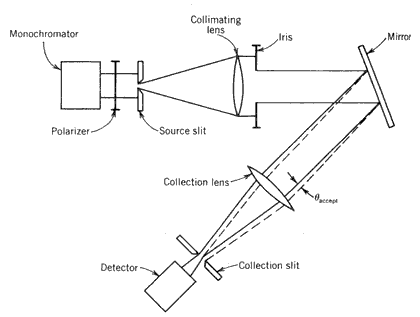
Figure 8.22 Measurement of specular reflectance
Non-specular reflectance is measured by use of a device that integrates the amount of light reflected by the surface in all directions.
An example of a specular reflector is a highly polished silver mirror that gives a clear undistorted reflected image. An example of a diffuse non-specular reflector is snow that yields no reflected image. The properties of curved mirrors to concentrate solar energy through specular reflection are examined in the following paragraphs.
It is important to recognize that, for a solar concentrator, specular reflection of the entire terrestrial solar spectrum is important. Not all materials exhibiting high specular reflectance reflect equally well at all wavelengths. The terrestrial solar spectrum is reported in Figure 2.10. Figure 8.23 shows the specular reflectance of several materials as a function of wavelength and illustrates why silver is widely used as a reflector material for solar collectors. Gold, for example, has a very high reflectance in the IR spectrum, which leads to its use as a radiation barrier in thermal insulation applications. However, it absorbs in the blue part of the visible spectrum (hence its color), decreasing its effectiveness as a solar reflector. The specular reflectance of several materials integrated over the entire solar spectrum are given in the Appendix.

Figure 8.23 Specular reflectance of selected materials. Ag, silver; Al, aluminum; Au, gold
Mirrors used in solar concentrators are frequently back-surface or second surface mirrors (i.e., the reflector surface is behind a protective sheet of glass or plastic). When light passes through a material, part of the light energy is absorbed. The absorption of light by transparent materials is an important factor in the design of the mirrors used in solar concentrators. Figure 8.24 is an example of a back-surface reflector. Since the light beam must traverse the thickness of the protective layer twice (once on incidence and again on reflection), any material that absorbs light can significantly reduce the solar energy reaching the receiver. The ability of a material to transmit light is characterized by its transmittance.
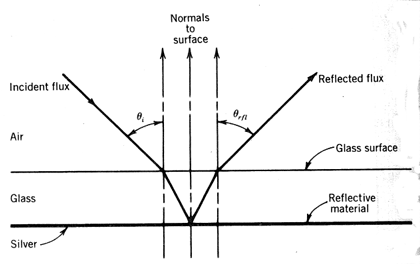
Figure 8.24
A back-surface reflectorTransmittance
(τ). The ratio of the radiant flux transmittedAs in the case of reflectance, transmittance can be either specular or diffuse. Light transmission through a homogeneous material such as glass or clear plastic is typically specular in that the transmitted ray follows Snell's law (Equation (8.54). A translucent material such as fiberglass may have high transmittance but localized discontinuities (e.g. glass fibers) that scatter the light, giving rise to a diffuse non-specular transmittance. Since solar concentrators typically employ only materials having high specular transmittance, the term "transmittance" in this book refers only to specular transmittance unless specified otherwise.
The ability of a material to transmit light is frequently a function of the wavelength of the light. Figure 8.25 shows the reflectance of back-surface glass mirrors with varying amounts of iron present as Fe2+. Since Fe2+ absorbs light in the visible part of the spectrum, the transmittance of glass (reflectance of a mirror) for the solar spectrum decreases with increasing concentrations of Fe2+. Thus, low-iron (i.e., 0.06 percent Fe2+ or less) glass and glass manufactured in a manner to convert Fe2+ to Fe3+, which does not absorb strongly in the solar spectrum, is of growing interest. In addition, thin mirrors are of interest since reduction of the path length that the light must traverse through the glass will reduce losses that are due to light absorption by the glass.
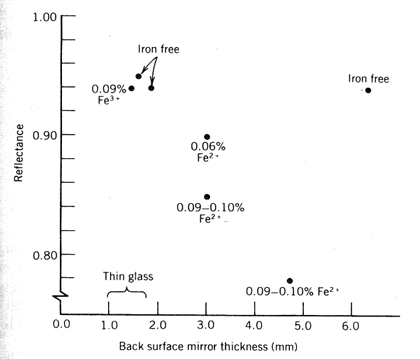
Figure 8.25 Effect of iron concentration on glass mirror reflectance (Clark, 1981).
8.6.2 Lenses
Lenses operate on the principle of Snell's Law. In particular, materials such as glass and clear plastics are used to refract the incident light, transmit the light specularly through the lens medium, and then refract the light again as it leaves the lens. Properly oriented, a curved lens is capable of refracting the parallel rays of the sun and concentrating the image on a receiver as shown in Figure 8.26. The optics of Fresnel lenses are discussed further in Section 8.7.
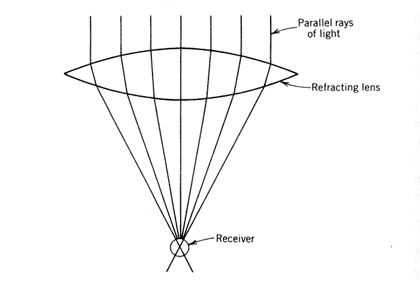
Figure 8.26 A concentrating lens.
8.6.3 Total Internal Reflection
An interesting consequence of Snell's law is the occurrence of total internal reflection. Total internal reflection can occur when light passes from a medium of high index of refraction to a medium of low index of refraction. Consider, for example, the passage of light from glass to air as shown in Figure 8.27. Total internal reflection occurs, as shown, when θrfr equals 90 degrees. Therefore, the incidence angle θi at which total internal reflection will occur can be calculated using Equation (8.54).
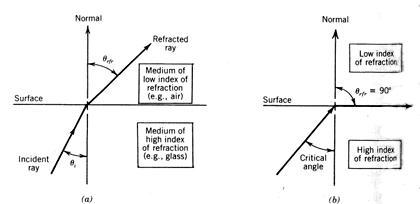
Figure 8.27 Total internal reflection: (a) refraction; (b) total internal reflection.
Example
: Calculate the angle at which total reflection of light passing from glass to air occurs.Thus, for incidence angles equal to or greater than 42 degrees, light passing from glass, with an index of refraction of 1.5, to air, with an index of refraction of 1.0, will undergo total internal reflection. This is termed the critical angle of the glass-air interface. Note that there is no critical angle for light passing from a medium of low index of refraction to a medium of high index of refraction.
8.6.4 Dielectric Reflection and Antireflection Coatings
In the discussion of reflection given above, there was no discussion of reflection from, for example, an air-glass interface. Reflection does occur, of course, as we all have observed when looking at a glass window. This is called the dielectric reflection. Referring to Figure 8.28, the fraction of the incident beam that is reflected at the interface is given by (Smith , 1966)
(8.57)
where the angles and
are as defined in Figure 8.28.
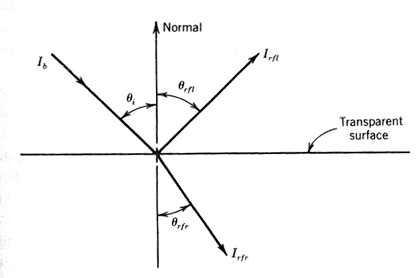
Figure 8.28
Dielectric reflection - definition of angles.The first term in Equation (8.57) gives the fraction of the incident beam polarized in the plane of incidence, and the second term gives the fraction polarized in the plane normal to the plane of incidence. Figure 8.29 is a plot of the reflection from a single air-glass interface as a function of incidence angle. Note that at
where
N1 and N2 are the refractive indices of the two media.
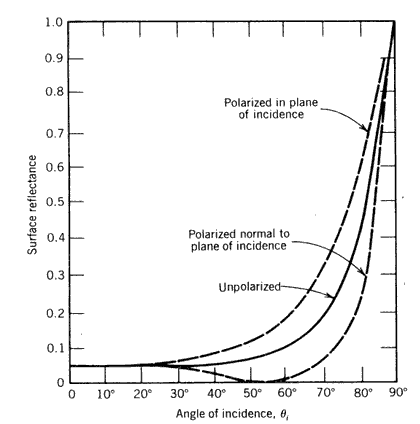
Figure 8.29 Effect of incidence angle on dielectric reflection from air-glass interface (Smith, 1966).
Optical coatings, so-called antireflection coatings, have been developed to reduce reflection from the air-glass interface in order to improve optical transmission. Such optical coatings have been used on the glass envelopes surrounding the receiver tubes of solar thermal concentrators.
One method of preparing antireflection glass surfaces is by etching the surface (Elmer and Martin, 1979). Antireflection surfaces on alkali-borosilicate glasses can be produced by exposing the glass surface to dilute acid solutions containing low concentrations of etchants, such as ammonium fluoride or ammonium bifluoride.
These solutions selectively extract soluble oxides within the surface layer, leaving a hydrated porous layer, largely silica, at the surface of the glass. The resulting surface layers are unique in that they maintain low reflectance losses in both the visible and the near-infrared. The reduction in dielectric reflectivity is attributable to a variable refractive index gradient caused by the interconnected pores of the silica-rich surface layer. The process is applicable to glasses that exhibit selective solubility in hot acid solutions. Etching has been used to produce an antireflection surface on the glass envelope surrounding the receiver in parabolic troughs (Anonymous, 1981). Figure 8.30 shows the transmittance of borosilicate glass treated in this manner.
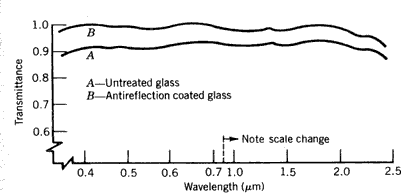
Figure 8.30
Transmittance of glass with antireflection coating (Elmer and Martin, 1979).
Fresnel (pronounced
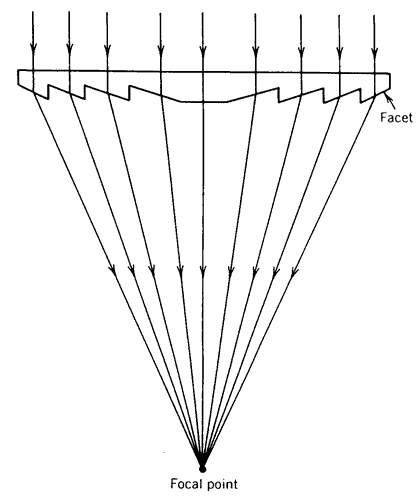
Figure 8.31
Idealized Fresnel lens.Several factors limit the effectiveness of Fresnel lenses. The most serious is, perhaps, the sharpness of the facets that can be produced. Any manufacturing process will produce slightly rounded facets as shown in Figure 8.32. Any ray striking the back side of a facet (e.g., ray 1) or the tip or valley of a facet (e.g., rays 2 and 3, respectively), is not properly directed to the receiver. The total fraction of the aperture area represented by these features is ineffective and reduces the ability of a Fresnel lens collector to perform efficiently.
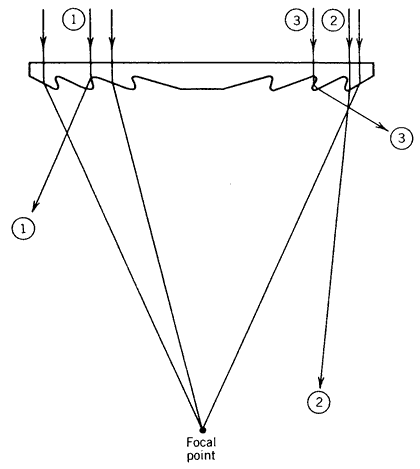
Figure 8.32 Problems associated with Fresnel lenses
Another feature that limits the performance of a Fresnel lens (or any other lens, for that matter) is dielectric and internal reflection (see Section 8.6). As the angle of incidence of light on a facet increases, the quantity of light reflected due to dielectric reflection increases. Figure 8.29 shows the reflection of light from an air-glass interface. Note that as the angle of incidence approaches 42 degrees, total internal reflection occurs for a glass lens. Thus the edge facets of a Fresnel lens are less effective than facets closer to the center of the lens. The effect is similar for plastic lenses since they have indices of refraction similar to glass (see Appendix D).
A more serious factor limiting the use of refractive optics is the need to track the lens about two axes. This is necessary to keep the concentrated image focused on a receiver that is fixed with respect to the lens. This is true even in the case of a linear lens. Figure 8.33a shows that as the incident rays are inclined (e.g., Ray l), in the plane of curvature, the refracted rays move. Thus, as would be expected, a minimum of single-axis tracking is required with a linear Fresnel collector.
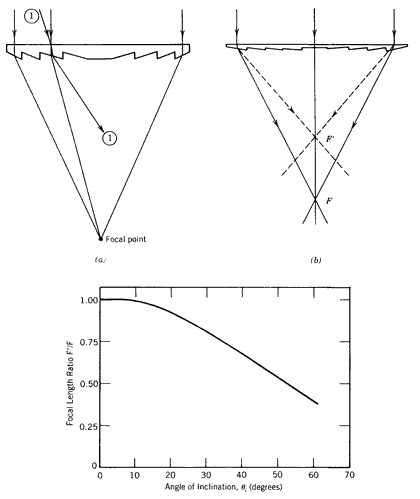
Figure 8.33 Two-axis tracking requirements for Fresnel lenses. (a) Effect on refracted beam inclined to lens aperture in the plane of curvature; (b) effect on refracted beam inclined along linear axis of lens. Solid line is in plane of paper (focus
F). Dashed line is out of plane of paper (focus F’); (c) change in focal length of linear Fresnel lens when incident rays inclined at an angle along the linear axis of the lens. Reprinted with permission from Solar Energy Technology Handbook, Marcel Dekker, New York (1980).However, a somewhat more subtle effect also due to refraction, occurs if the incident ray is inclined along the linear axis of the Fresnel lens. This is illustrated in Figure 8.33b and 8.33c. The net result, over the entire lens, is the creation of a new focal line for the lens that is above the normal focal line. To maintain the refracted image focused on a receiver that is fixed with respect to the lens, therefore, one must track a Fresnel lens collector (or any lens system) to maintain the incident light normal to the lens aperture. This requires two-axis tracking.
In summary, the impact of the geometric optics of cylindrical and parabolic mirrors is that parabolic optics allow construction of high rim-angle troughs that need track about only one axis, whereas low rim-angle cylindrical troughs may be constructed that need not track at all to maintain a moving linear focus. These discussions of tracking requirements involve only focusing considerations. Complete two-axis tracking of the collector aperture will, of course, increase the amount of insolation incident on the collector aperture by elimination of the cosine effect. The magnitude of this effect for the various tracking modes is discussed in Chapter 4.
References
Abramowitz and Stegun (1970), Handbook of Mathematical Functions, National Bureau of Standards, Washington D.C.
Anonymous (1981), "Solar Thermal Monthly Progress Report," Sandia National Laboratories, Albuquerque.
Bergeron, K. D., and J. M. Freese (1981), "Cleaning Strategies for Parabolic Trough Collector Fields; Guidelines for Decisions," SAND81-0385, Sandia National Laboratories Albuquerque.
Clark, N.H. (1981), "Material Design Considerations for Silvered Glass Mirrors," in Proceedings of the Line-Focus Solar Thermal Energy Technology Development-A Seminar .for Industry, p. 409, SAND80-1666, Sandia National Laboratories, Albuquerque.
Elmer, F. H., and F. W. Martin (1979), "Antireflection Films on Alkali-Borosilicate Glasses Produced by Chemical Treatments," Am. Ceramic Society Bulletin 58, 1092.
Kutscher, C. T., and R. Davenport (1981), "Preliminary Results of the Operational Industrial Process Heat Field Tests," SERI/TR-632-385R, Solar Energy Research Institute, Golden, CO, June.
Harris, J. A. and W. S. Duff (1981), "Focal Plane Flux Distribution produced by Solar Concentrating Reflectors" Solar Energy 27 (5), 403.
Larsen, L. M., and J. M. Freese (198l), "Solar Collector Cleaning Study," in Proceedings of The Line-Focus Solar Thermal Energy Technology Development - A Seminar for Industry, p. 189, SAND80-1966, Sandia National Laboratories, Albuquerque.
Pettit, R. B., and E. P. Roth (1980), "Solar Mirror Materials: Their Properties and Uses in Solar Concentrating Collectors," in Solar Materials Science, L. E. Murr, ed., p. 171, Academic Press, New York.
Smith, W. J. (1966), Modern Optical Engineering, McGraw-Hill, New York.
Torkelson, L., and D. L. Larsen (1981), "1980 Annual Report of the Coolidge Solar Irrigation Project," SAND80-2378, Sandia National Laboratories, Albuquerque.