5. ______________________________
Solar Collectors
Solar collectors capture incident solar radiation energy and either convert it to heat (thermal energy) or directly to electricity (photovoltaic cells). In Chapter 4 we developed the equations necessary to predict the amount of solar irradiance or energy falling on a solar collector. We looked at different cases of tilting and tracking the collectors to optimize the solar input. In this chapter, we study how a solar collector absorbs and converts solar energy into thermal energy or electricity as in the case of photovoltaic panels. The topics covered in this chapter are:
We will first look at solar thermal collectors and then at photovoltaic modules. Here we derive the energy balance for thermal collectors, without regards to the specific type; that will be dealt with in the following chapters. We will also understand the energy balance for a photovoltaic module, without going into the details of the electro-physics of the processes happening within the cells.
Prior to an examination of specific collector concepts, this chapter shows the development of a widely used yet simple model for prediction of the thermal energy output (i.e., performance) of various solar collectors. The model is applicable to all (including the central receiver with some extension) collector concepts and hence is discussed separately from any one collector concept to avoid the misunderstanding that the model is useful only for that one concept.
Although the presentation of a model for computation of collector performance before discussion of the individual collector design concepts may seem strange, system design can proceed if certain thermodynamic characteristics are known, without detailed knowledge of what the collector looks like. Usually, collector performance is determined from experimental data of prototype hardware. A particularly important feature of the performance models discussed in this chapter is that it exploits such data and extends it to different operating conditions. If experimental data are not available, the designer must resort to an analytical description of the collector’s performance, which is always risky.
In a similar manner, a simple model of photovoltaic panel performance is presented. Like the thermal collector performance model, it is based on experimental data that is modified for operating parameters different from a ‘standard’ condition.
5.1 Thermal Collector Capture and Loss Mechanisms
To perform an energy balance on a solar thermal collector, one usually isolates the surface that absorbs the incoming radiation, and balances energy inflow and outflow to and from it. In a flat-plate collector, this is called the ‘absorber plate’ and for a concentrating collector, it is often called the ‘receiver’. In subsequent chapters we will describe many details of construction, surfaces for each type of collector, but for now, this is not important. The energy balance on a solar collector absorber or receiver can be written as;
where:
- rate of ‘useful’ energy leaving the absorber (W)
- rate of optical (short wavelength) radiation incident on
absorber (W)
- rate of thermal energy loss from the absorber (W)
The ‘useful’ energy for a solar thermal collector is the rate of thermal energy leaving the collector, usually described in terms of the rate of energy being added to a heat transfer fluid passing through the receiver or absorber, i.e.:
where:
- mass flow rate of heat transfer fluid (kg/s)
cp - specific heat of heat transfer fluid (J/kg.K)
Tout - temperature of heat transfer fluid leaving the absorber (K)
Tin - temperature of heat transfer fluid entering the absorber (K)
These losses are shown schematically in Figure 5.1.
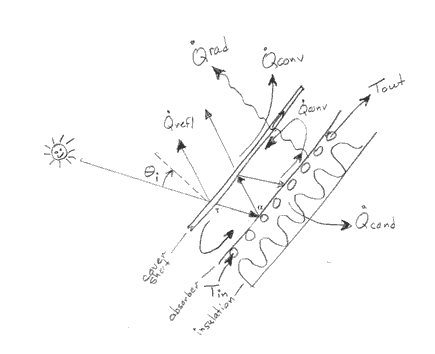
Figure 5.1 Energy balance on a solar collector absorber / receiver.
The rate of optical (short wavelength) radiation incident on absorber/receiver will be the solar irradiance resource for that type of collector and its tracking (global (total) solar irradiance for a flat-plate collector and direct (beam) solar irradiance for a concentrating collector). Since the capture area of the collector may not be aimed directly at the sun, this resource must be reduced to account for the angle of incidence as described previously in Section 4.1. The area of the collector on which the solar irradiance falls is called the aperture (opening) area of the collector. The incident solar resource then is:
(5.3)
where:
Ia - solar irradiance entering the collector aperture (global (total) or direct (beam))(W/m2)
Aa - aperture area of the collector (m2)
This solar resource is reduced by a number of losses as it passes from the aperture of the collector to the absorber. These processes depend on the type and design of the specific collector, but here we include the important optical loss mechanisms, and will drop the unimportant terms in future chapters as we discuss specific types of collectors. The rate of optical (short wavelength) energy reaching the absorber or receiver is the product of the incoming solar resource multiplied by a number of factors, all less than 1.0 describing this reduction:
where:
- capture fraction (fraction of reflected energy entering or impinging on receiver)
- reflectance of any intermediate reflecting surfaces
- transmittance of any glass or plastic cover sheets or windows
- absorptance of absorber or receiver surface
The first two terms above apply only to concentrating collectors. The capture fraction is a measure of both the quality of the shape of the reflecting surface, and the size of the receiver. Often this is described in terms of ‘spillage’ i.e. the fraction of reflected energy not impinging on or entering the receiver. A poorly shaped concentrator, or a receiver too small will make this number considerably less than 1.0. An analytical method for calculating this term is presented in Chapter 8, Concentrator Optics.
Reflectance is a property of any reflecting surface associated with the collector. The importance of this property will also will be discussed in more detail in Chapter 8 (Concentrator Optics). Properly designed concentrators will have capture fractions of 0.95 or higher, and silver/glass mirrors can have a reflectance of 0.94 and new aluminum reflecting surfaces have a reflectance of about 0.86.
The transmittance is the fraction of solar radiation passing through all transparent cover material that sunlight passes through on its way to the absorber. Cover sheets of glass or plastic are used on flat-plate collectors, above the absorber to reduce convective heat loss.
For parabolic trough collectors a glass tube surrounds the absorber tube for the same reason. High-temperature cavity receivers may incorporate a quartz glass cover to keep the gas in the receiver separate from outside air or to permit pressurization of the gas within the cavity. In all cases, the use of a cover sheet reduces the solar radiation passing to the receiver/absorber. Their benefit for reducing heat losses from the absorber must at least balance this reduction.
The transmittance in Equation (5.4) is the average overall transmittance and represents the total reduction in transmitted energy in the solar spectrum by all covers. For example, flat-plate collectors may have two or more cover sheets, sometimes of different materials, with the transmittance, τ being the product of each individual cover transmittance.
Transmittance of the cover also depends on the wavelength of light passing through it. Glass for example transmits most radiation in the visible spectrum, but does not transmit much in the infrared region. Therefore, an absorber covered with glass will receive most of the incoming, short wavelength radiation, but will not transmit much of the long wavelength radiation loss coming from the absorber. This characteristic of glass is the reason that glass greenhouses loose very little energy at nighttime. Carbon dioxide buildup gives our atmosphere a similar property and therefore the name ‘greenhouse effect’.
On the other hand, plastic covers have high transmittance values at very long wavelengths. Solar collectors using plastic covers can be used for nighttime cooling since radiation loss to the nighttime sky can be significant. This is also why greenhouses in warm climates use plastic rather than glass as a cover. Without nighttime long-wavelength radiation loss, the average temperatures would be too high for optimal plant growth.
The absorption term represents the fraction of solar energy incident upon the surface, that is absorbed (the remainder being reflected). A good black surface can have an absorption of greater than 0.98, however, as surfaces degrade, this value can decrease. It is important to point out that this property is for radiation in the solar or ‘visible’ spectrum. For most real surfaces, the absorption varies as a function of the wavelength of the incident energy. We will discuss below that there is a class of surfaces used in solar collectors, called ‘selective surfaces’ that have a higher absorptance in the visible spectrum than at longer wavelengths, thereby reducing thermal radiation loss.
In summary then, when performing an energy balance on the absorber plate or receiver of a solar collector, there are four important mechanisms that reduce the amount of solar energy that is incident on the collector aperture; imperfect reflection, imperfect geometry, imperfect transmission and imperfect absorption. This is a general statement, and different collector types will either include or not include these losses depending on the design.
Once the solar energy resource (short wavelength radiation) has made its way down to the surface of the absorber or receiver of a collector, it raises the temperature of the absorber above ambient temperature. This in turn starts a process of heat loss from the absorber as with any surface heated above the temperature of the surroundings. These loss mechanisms are convection, radiation and conduction, and all are dependent on, among other things, the difference in temperature between the absorber and the surroundings.
(5.5)
Because a solar thermal collector is designed to heat a fluid, there is a balance between the rate of heat being removed by the heat transfer fluid and the heat loss by radiation, convection and conduction as defined by Equation (4.1). Since heat loss increases with temperature, this balance between heat removal and heat loss defines the operating temperature of the collector.
If the heat transfer fluid removes too much heat, the temperature of the absorber decreases, reducing heat loss. If not enough heat is removed from the absorber, the absorber temperature increases, increasing the rate of heat loss. This can pose a major problem for concentrating collectors, because when not enough heat is being removed (as can happen if the flow of heat transfer fluid is interrupted), the temperature of the absorber can increase to its melting temperature.
Convection Loss - Convective heat loss of a solar collector receiver is proportional to the surface area of the absorber or receiver, and the difference in temperature between the absorber surface and the surrounding air. It can be written in general terms as:
(5.6)
where:
- average overall convective heat transfer coefficient (W/m2.K)
- surface area of receiver or absorber (m2)
- average temperature of receiver (K)
- ambient air temperature (K)
As with the other heat loss equations below, this is a simplified, instructive model. Usually there are a number of convective processes that cause an absorber or receiver to loose heat to the surroundings. For example, a flat-plate collector often has a glass cover sheet between the absorber plate and outside ambient air. There is one convection process between the hot absorber and the cover sheet, and a second between the cover sheet and outside air. Also, wind increases the heat transfer coefficient on the cover sheet and must be included in any serious analysis of convective heat loss.
For parabolic dish concentrators, the absorbing surface is typically placed inside of a cavity. This protects it from wind, and naturally driven air currents. Little is known about convective heat loss from an open cavity, but it is clear that the position of the cavity and its internal temperature, along with wind speed and direction all affect the rate of heat loss from a cavity (Stine & McDonald, 1989, Paitoonsurikarn et. al., 2003).
Finally, the average temperature of the absorber / receiver, is not a fixed or measurable quantity. The temperature of the absorber / receiver near the heat transfer fluid inlet will be lower than near the outlet, and both will be less than intermediate surfaces not in contact with the heat transfer fluid. Further, since convection is a surface phenomenon, also is driven by the surface temperature, this temperature may be that of a paint or coating rather than the metal below.
Even with all of these imperfections, it is instructive to consider the convective heat loss as being proportional to surface area and the difference between some average temperature, and ambient temperature.
Since convective heat loss is the major heat loss term for most solar collectors, inventors and designers have incorporated many features to collector design to reduce this term. Examples that will be discussed under the different collector designs are; multiple transparent cover sheets for flat-plate collectors, glass tubes surrounding linear absorbers with a vacuum drawn in the intervening space, concentration of solar energy so that the absorber area is small relative to the capture area, absorbers within cavities incorporating glass windows, just to name a few.
Radiation Loss - Radiation heat loss is important for collectors operating at temperatures only slightly above ambient, and becomes dominant for collectors operating at higher temperatures. Figure 5.2 illustrates this transition for a black vertical surface in still air. The rate of radiation heat loss is proportional to the emittance of the surface and the difference in temperature to the fourth power. Described in equation form, we have:
(5.7)
where:
- emittance of the absorber surface (or cavity in the case of a cavity receiver)
- the Stefan-Boltzmann constant (5.670 × 10-8 W/m2 K4)
- the equivalent black body temperature of the sky (K)
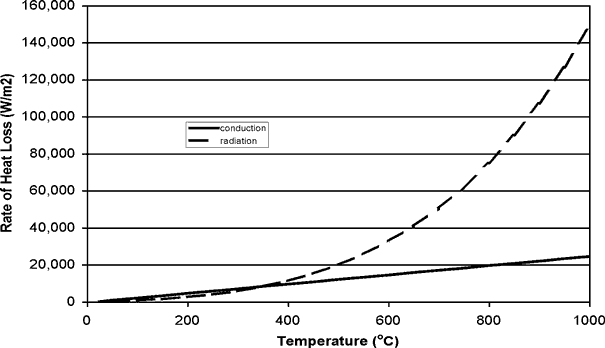
Figure 5.2 Comparison of radiation and convection heat loss for a black, vertical surface in free air at 25oC.
Terms in this equation over which the collector designer has some control, are the surface emittance and receiver. Surfaces that have a low emittance often have a low absorptance as well, reducing the absorbed solar energy as described in Equation (4.4). However there is a class of surface coatings called ‘selective coatings, that have low values of emittance when the surface is at relatively low temperatures, but high values of absorptance for solar energy. These surfaces are discussed in Section 4.1.4 below.
The other term, which may be minimized, is the receiver surface area. As with convection loss, concentration of solar energy is the main design tool for reducing radiation heat loss by reducing receiver surface area. In addition, cavity receivers can be used since they have small openings through which concentrated solar energy passes, onto larger absorbing surfaces.
Since solar collectors operate out of doors, and generally face the open sky, they exchange radiation with the sky. The equivalent radiation temperature of the sky depends on the air density and its moisture content. When the relative humidity is high and at sea level, the sky temperature can be assumed to be the same as ambient air temperature. However, for low relative humidity or at high altitudes, the sky radiation temperature can be 6 to 8oC less than ambient temperature. Of course if there is no atmosphere as with space applications, the equivalent sky temperature approaches 0K.
Conduction Loss - The final mode of heat loss to consider in collector design is heat conduction. This is generally described in terms of a material constant, the thickness of the material and its cross-section area:
(5.8)
where:
- equivalent average conductance (W/m.K)
- the average thickness of insulating material
Conduction loss is usually small compared to convection and radiation losses and therefore is combined with the convection loss term in most analyses. However, it is displayed here for completeness, and to emphasize the importance of ensuring that this mode of heat loss is minimum in any collector design.
In flat-plate collectors, the sides and back surface of the absorber plate should incorporate good insulation (low k) and the insulation should be thick enough to render this heat loss insignificant.
Another important mode of conduction loss is the way the high-temperature absorber is attached to the frame and support structure. Use of low conductance materials such as stainless steel can reduce conduction loss into the frame or support casing. However, since most design issues around conduction can be handled without reducing the solar input, the term is generally combined with the convective heat loss term.
In order to provide a single expression for the useful energy produced from a solar collector based on an energy balance of the receiver or absorber, we can combine Equations (4.1) through (4.8) into a single equation. This equation will be repeated in the next few chapters as we develop an understanding of how and why specific types of collectors are designed the way they are.
where:
- combined convection and conduction coefficient (W/m2K)
This equation states that the rate of useful energy produced by a solar collector equals the optical (short wavelength) energy absorbed on the absorber surface, minus the rate of heat loss from the absorber. We have combined the convection heat loss term with the convection term for simplicity.
At this point in developing an understanding of solar energy capture and loss mechanisms, we have introduced two important properties in solar collector design, absorptance, α and emittance, ε. A category of surfaces called ‘selective surfaces’ has been developed to optimize these parameters for the collection of solar energy and it is important to understand their physical principles.
Looking at Equation (4.9), one can see that, to maximize the useful heat collected by a solar collector, the absorber or receiver of a solar collector should have a high absorptance and a low emittance. However, we remember from radiation heat transfer theory that, at least for black body and gray surfaces, the absorptance equals the emittance
. However for all surfaces, Kirchoff’s Law states that they are equal only for radiation at a specific wavelength, not as an average property integrated over a spectrum. Kirchoff’s law states that:
(5.10)
where the subscript indicates that these are ‘spectral’ properties and must be integrated over all wavelengths to represent the properties used in Equations (4.4) and (4.7). If the spectrums are different, the integrated properties can be different.
In solar collectors, the spectrum of the energy being absorbed is from a 6,050K black body emitter with peak intensity at a wavelength of 0.48 microns (see Table 2.3). The spectrum of the energy being emitted by the absorber / receiver is defined by the temperature of the absorber surface, Tr which is considerably less. For example if the receiver surface temperature is 80oC, the peak intensity is at a wavelength of 8.21 microns.
Selective surfaces have a high absorptance (and emittance) for short wavelength (visible) light and have low average absorptance and emittance for long wavelength radiation (thermal or infra-red radiation). They do not violate Kirchoff’s law, however, we say that they have ‘high absorption and low emittance’ meaning high absorption for short wavelength radiation, and low emittance for long wavelength radiation. The end result is a surface that absorbs solar energy well, but does not radiate thermal energy very well.
The concept of a selective surface is illustrated in Figure 5.3. Consider a hypothetical surface with 0.95 absorptance at wavelengths shorter than 5 microns and 0.25 for longer wavelengths. Since 99.5% of solar energy occurs at wavelengths below 5 microns as discussed in Chapter 2, Section 2.1.2, the effective absorptance of such a surface is 0.945. The integrated emittance for this hypothetical surface depends on its temperature. If this surface is 80oC as is typical for hot water system collectors, 99.1% of its radiant energy is at wavelengths above microns and the integrated emittance for this surface is 24.8%.
On the other hand, the effect of using a selective surface is less dramatic on higher temperature absorbers. If the absorber surface is at a temperature of 700oC as is typical for receivers in parabolic dish concentrating collectors, only 43.6 % of its radiated energy is at wavelengths above 5 microns and the integrated emittance is 64.5%.

Figure 5.3 Radiation properties of a hypothetical selective surface.
Selective absorbers have been developed that employ composite coating to produce absorbers with the combined properties of high absorptance in the solar spectrum and low emittance in the IR part of the spectrum.
Several coatings have been examined for potential application as selective absorbers. Perhaps the most widely used selective surface in thermal collectors is black chrome. Typically, a thin (2-3
μm thick) black chrome coating is electro-deposited on a mild steel receiver tube that has been electroplated with 25 μm of bright nickel.The coating is deposited, as microscopic particles of chromium metal that, because of their geometry, effectively trap the incident light, making the coating look black. Although the black chrome coating is highly absorbing in the visible spectrum, it is transparent in the IR region. Thus the receiver takes on the lower emittance of the bright nickel substrate. The resultant composite bright nickel-black chrome coating thus has high absorptance (approximately equal to 0.95) for the incident solar radiation and low emittance (less than 0.25) in the infrared region.
5.1.5 Parabolic Trough End-loss
One final loss mechanism to consider, which is particular to parabolic troughs, is called end-loss. This is the fraction of energy being reflected from the trough that falls beyond the receiver. This loss is proportional to the angle of incidence. End-loss will be illustrated in Chapter 9 of this text.
5.2 Photovoltaic Panel Capture and Loss Mechanisms
An energy balance on a photovoltaic panel provides less useful information to the solar energy system designer. However since the photovoltaic cell efficiency decreases with increases in panel temperature, it is important for the rate of heat loss from the panel to be high rather than low! In other words, while the solar thermal panel must be hot to provide useful energy, photovoltaic panels should remain cool to maximize their output of useful energy (electricity in this case).
An energy balance of a photovoltaic cell incorporated within a panel can be written as:
where:
i
- electrical current through the cell (amps)v
- voltage across the cell (volts)and the rate of optical radiation incident on the cell and the rate of thermal energy loss from the cell have the same meaning as in Equation (5.1).
There is a physical limit to the fraction of useful energy that can be produced from the incident optical radiation. Depending on the type and design of the cell this can be from 1 percent to 30 percent. This requires that the rest of the remaining 70% to 99% of the incident energy, be lost through heat loss mechanisms.
Just as Equation (4.4) was instructive in understanding the potential loss mechanisms for a thermal collector, it likewise describes the potential loss mechanisms for a photovoltaic cell. In a concentrating photovoltaic panel, energy incident on the cell is reduced by the reflectance, ρ of the intermediate reflecting surfaces, and the fraction of reflected energy that falls on the cell, Γ. The transmittance, τ of the cover sheet used to physically protect the cell surface and to keep moisture and oxygen away from the electrical contacts, further reduces the optical energy incident on the cell.
Heat loss from the panel follows the same three paths, convection, radiation and conduction. Optimizing those factors that increase heat loss without increasing cell temperature are important for well designed photovoltaic panels. Maximizing heat loss for concentrating PV collectors is more difficult due to the reduced cell surface area resulting from concentration.
The detailed energy balance for a photovoltaic cell in a panel can be written in a manner similar to Equation (4.9), replacing the receiver/absorber temperature term with the temperature of the cell:
(5.12)
where:
Tc- temperature of the cell (K)
Ac - area of the cell surface (m2)
5.2.4 Photovoltaic Panel Performance
Performance of a photovoltaic panel or concentrating photovoltaic collector can be described in terms of its voltage and current output. The electrical power output from the panel is the product of these two variables. Voltage and current vary with the intensity of the solar irradiance and the temperature of the cell, all of which are described in the following figures. These figures were derived from real data taken on a commercial photovoltaic panel of approximately 0.65 m2. However, only the trends are important here and the solar designer should obtain similar information from the manufacturer of the specific panel or concentrator to be used in their design.
The I-V Curve - The fundamental performance of a photovoltaic panel is represented by Figure 5.4, called an I-V curve. It is a plot of the voltage across the panel for different values of current. Since the voltage is a product of the current and the load resistance, lines of constant load resistance are shown to complete the description.
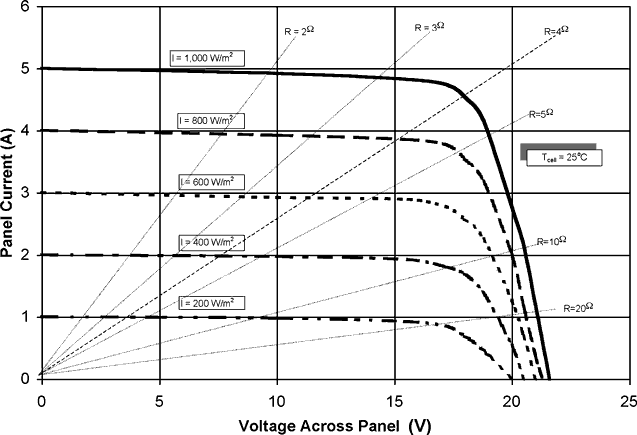
Figure 5.4 Photovoltaic panel output current as a function of the voltage across the panel. These I-V curves are shown for different levels of insolation. Also superimposed on graph are lines of constant load resistance. Data are for a cell temperature of 25oC and an air mass of 1.5.
At low values of load resistance, the current is a maximum and the voltage across the cell approaches zero. This condition is equivalent to a short-circuit across the cell, and the current output at zero voltage is called the short-circuit current or
Isc. This current is a function of the size of the photovoltaic cell, and the number of cells connected in parallel.It can also be seen that the short-circuit current is also directly proportional to the level of solar irradiance. This characteristic is why photovoltaic cells can be used as a transducer to measure solar irradiance as discussed in Chapter 2.
As the load resistance increases, the current decreases slightly until a point is reached where the cell can no longer maintain a high current level, and it falls to zero. The point at which the panel current falls to zero represents an infinite resistance or an open circuit. The voltage across the panel at zero current is called the open-circuit voltage, Voc, and represents the output of the unloaded panel. Note that the open-circuit voltage varies only a small amount as a function of solar irradiance (except at very low levels).
A single silicon photovoltaic cell produces an open-circuit voltage of slightly over 0.55 volts. The voltage produced by a photovoltaic panel is a function of how many cells are connected in series. In the case of the panel described below, there must be about 36 photovoltaic cells connected in series in order to produce over 20 volts.
Peak Power Point
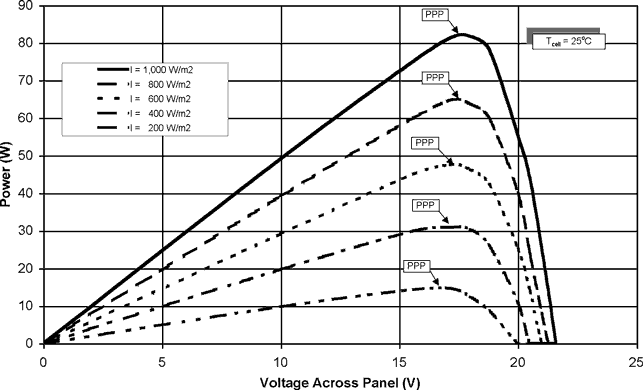
Figure 5.5 Power output of a photovoltaic panel at different levels of solar irradiance. The notation PPP defines the peak power point. Data are for a cell temperature of 25oC and an air mass of 1.5.
Note that the peak power output occurs at a panel voltage of about 80% of the maximum open-circuit voltage, for a wide range of solar irradiance levels. In order to maintain maximum electrical power output from a photovoltaic panel, the load resistance should match this point. As can be seen on Figure 5.4, the load resistance must increase as solar irradiance decreases in order to maintain maximum power output from the panel.
Since the resistance of most electrical loads are fixed (except for electrical motors and batteries), special consideration must be taken in the system design to ensure that the maximum potential of the solar panel is utilized. There are electronic devices, called peak power trackers that ensure that the panels are operating close to their peak power point.
Cell Temperature Loss - An important characteristic of the photovoltaic cell is the reduction of output voltage as cell temperature increases. Figure 5.6 shows this characteristic for the photovoltaic panel described in Figures 5.4and 5.5. Although not obvious on this curve, the short circuit current increases slightly with temperature. Typical values for these changes are

Figure 5.6 Effect of cell temperature on photovoltaic panel output. Data shown are for an irradiance of 1,000 W/m2 and an air mass of 1.5.
All of the data presented so far have been for photovoltaic cells at a temperature of 25oC. In a real system design, this is seldom the case. Photovoltaic cells are usually encapsulated in a panel to provide rigidity and physical protection of the front surface. Since panels must reject 80% to 90% of the solar energy incident upon them, and usually this transfer is to the ambient air, both the air temperature and the wind speed and direction have great effects on this.
The concept of a normal operating cell temperature (NOCT) has been defined in order to provide some sense of the ability of a specific panel to reject heat and provides a design guideline for system performance analysis. Normal operating cell temperature is the cell temperature under ‘standard operating conditions’, ambient air temperature of 20oC, solar irradiance of 800 W/m2 and wind speed of 1 m/s. NOCT values are specific to a particular panel or collector, but generally are about 50oC for flat-plate panels.
All data presented above are for an air mass of 1.5 (AM=1.5). The concept of air mass was introduced in Chapter 2, Section 2.2.2. The air mass is an indication of the path length that solar irradiance travels through the atmosphere. An air mass of 1.0 means the sun is directly overhead and the radiation travels through one atmosphere (thickness). The air mass is approximately equal to the reciprocal of the cosine of the zenith angle and an air mass of 1.5 would represent a zenith angle of 48.2 degrees or an altitude angle of 41.8 degrees.
At this point in our discussion of how solar energy is collected, we will define the basic performance parameter, collector efficiency. We will then describe how this is measured and then how these measurements can be combined into an analytical model to predict collector output. This is done in general terms, applicable to flat-plate and concentrating collectors for either thermal or photovoltaic applications.
The solar energy collection efficiency,
where:
= rate of (useful) energy output (W)
Aa
= aperture area of the collector (m2)Ia
= solar irradiance falling on collector aperture (W/m2)This general definition of collector efficiency differs depending on the type of collector. The rate of useful energy output from thermal collectors is the heat addition to a heat transfer fluid as defined by Equation (5.2) whereas the useful energy output of a photovoltaic collector is electrical power defined in Equation (5.11). The incoming solar irradiance falling on the collector aperture, Ia, multiplied by the collector aperture area represents the maximum amount of solar energy that could be captured by that collector.
In some of the development that follows, we will use the concept of optical efficiency. The optical efficiency of a solar collector is defined as the rate of optical (short wavelength) energy reaching the absorber or receiver, divided by the appropriate solar resource. Dividing Equation (4.3) by Equation (4.4), we have for optical efficiency;
This term is often used in separating out the non-thermal performance of a solar collector. It also forms the maximum limit for collection efficiency as will be seen in our discussions below.
Since flat-plate collectors (both thermal and photovoltaic) are capable of absorbing both direct (beam) and diffuse solar irradiance, the appropriate aperture irradiance is the global (total) irradiance falling on the collector aperture.
(5.15)
where It,a is the global irradiance on a collector aperture.
Equations for calculating global (total) irradiance on an aperture were the subject of Chapter 4, Section 4.2.1 and for the general case we may use Equation (4.29). Various schemes of orientation and tracking were discussed in Section 4.1 and may be applicable to determining the angle of incidence. Equation (4.29) includes both direct (beam) and scattered and reflected energy.
Adding the appropriate useful energy term to Equation (5.13) we have for thermal and photovoltaic flat-plate collectors, the following definitions of collector efficiency
Flat-plate thermal collectors:
(5.16)
Flat-plate photovoltaic collectors:
(5.17)
5.3.3 Concentrating Collectors
Concentrating collectors on the other hand can only concentrate direct (beam) solar irradiance and therefore the appropriate irradiance term is direct (beam) normal solar irradiance, reduced by the cosine of the angle of incidence. For two-axis tracking collectors, the angle of incidence is zero.
(5.18)
where Ib,a is the direct (beam) irradiance on a collector aperture.
Equations for calculating direct (beam) irradiance on an aperture were the subject of Chapter 4, Section 4.2.1 and for the general case we may use Equation (4.28). Various schemes of orientation and tracking were discussed in Section 4.1 and may be applicable in determining the angle of incidence. Equation (4.28) includes both direct (beam) and scattered and reflected energy.
Adding the appropriate useful energy term to Equation (5.13) we have for thermal and photovoltaic concentrating collectors, the following definitions of collector efficiency:
Concentrating thermal collectors:
(5.19)
and
Concentrating photovoltaic collectors:
(5.20)
5.3.4 Non-imaging Concentrators
One further caveat must be mentioned for non-imaging concentrators such as vee-troughs, conical concentrators and compound parabolic concentrators (CPC). Since these accept some diffuse solar irradiance, the appropriate Ia would be the direct (beam) normal, reduced by the cosine of the angle of incidence plus the circumsolar diffuse solar irradiance falling within the acceptance angle of that specific concentrator.
(5.21)
where the terms Id,aa and Ir,aa are the sky diffuse and reflected diffuse energy that are available within the acceptance angle of the non-imaging concentrator. The definition of these terms is beyond the scope of this book. However, this solar irradiance may be easily measured by reducing the tube length of a pyrheliometer and attaching this to the aperture of the non-imaging concentrator.
5.4 Models of Collector Performance
Models of collector performance that will predict collector output under varying solar irradiance, operating temperature and weather conditions, are important to the system designer. This type of model can be used in system performance prediction programs such as SIMPLES, to predict the output of the collector field.
The most prevalent solar collector performance model is called the ‘delta-T over I curve’ and permits prediction of useful energy out under varying solar irradiance, ambient temperature and system operating temperature. Although its required simplifications work well for low- temperature flat-plate collector systems, it has been modified for use with higher temperature systems as described below. This model has no applicability to photovoltaic collectors.
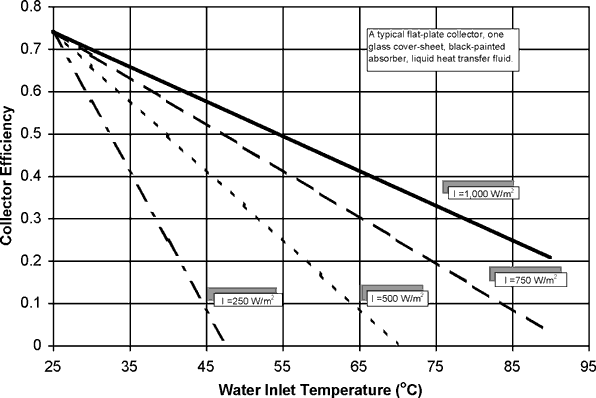
Figure 5.7 summarizes the performance of a typical flat-plate collector. Plots a) and b) show that, the rate of useful energy produced decreases as the temperature of the fluid entering the collector increases. As expected the higher the solar irradiance level, the higher the rate of useful energy produced. Curve b) shows the same data plotted in inverse order. Plots c) and d) show collector efficiency rather than useful energy produced. Curve c) shows that efficiency is independent of solar irradiance when fluid inlet temperature equals ambient temperature. This point defines the optical efficiency. Curves c) and d) can be combined into a single curve e) defining the relationship between collector efficiency, solar irradiance and fluid inlet temperature as described below.
5.4.1 Flat-plate Collectors, The
Curve
Starting with Equation (4.9), the following simplifications can be made for a flat-plate collector operating at low temperatures (below approximately 90oC):
There is no reflection of incoming solar irradiance and therefore
Γ and ρ are eliminated.The aperture area is the same as the absorber area (
Aa = Ar)Radiation heat loss can be combined with convection and conduction into a single overall heat loss coefficient,
UL (W/m2K). This coefficient is a constant for the particular collector being modeled. (Temperature dependence of this term due to natural convection and radiation causes non-linear affects to occur and will be discussed below).The average receiver panel temperature,
The appropriate solar irradiance resource for a flat-plate collector,
Ia is the global (total) solar irradiance on a tilted surface, It,βWith these simplifications, Equation (4.9), for normal incident solar irradiance becomes:
(5.22)
If it is further assumed that FR, τ, α, UL are constants for a given collector and flow rate, then the efficiency is a linear function of the three parameters defining the operating condition; solar irradiance, fluid inlet temperature and ambient air temperature. This is the single line shown on curve e) in Figure 5.7.
The slope of this line represents the rate of heat loss from the collector. For example, collectors with cover sheets will have less of a slope than those without cover sheets. The intercept of the line on the efficiency axis is sometimes called the optical efficiency. Most low-temperature solar collector performance data are presented in terms Equation (4.21). It
should be remembered that both of these terms are multiplied by the heat removal factor, FR making them a function of flow rate. Therefore the flow rate for any curve should be specified.

Curve a)
Curve b)

Curve c)
Figure 5.7 Performance of a typical flat-plate thermal collector (one glass cover, black-painted absorber, water transfer fluid and ambient temperature 25oC). Curve a) shows the performance as a function of the
There are two interesting operating points on Figure 5.7, curve a). The first is the maximum collection efficiency, called the optical efficiency. This occurs when the fluid inlet temperature equals ambient temperature. For this condition, the
The other point of interest on Figure 5.7, curve a) is the intercept with the
Curves b) and c) of Figure 5.7 are derived from curve a); the
Curve c) of Figure 5.7 shows the relationship of system output to the irradiance level. It shows that systems operating at low temperature levels (such as swimming pool heating systems) can derive heat from the sun at very low levels of irradiance. Higher temperature operating systems such as domestic hot water systems only derive energy from the sun when the irradiance level is high. Further study of curves b) and c) will reveal most of the important aspects of the thermal design of solar energy systems.
5.4.2 Parabolic Troughs, The Non-Linear
For parabolic trough collectors operating at higher temperatures, the above assumptions must be modified. In order to better approximate the temperature at which heat loss takes place, an average receiver temperature, is calculated as the average between the inlet and outlet fluid temperatures:
(5.23)
where:
Tin - incoming heat transfer fluid temperature (K)
Tout - outgoing heat transfer fluid temperature (K)
The curves produced during testing have significant non-linearity. Thus the
curve must be fit analytically. Typically this is done using an expansion of Equation (4.21) of the form
(5.24)
where the coefficients a and b are determined by a curve fit to test data.
The addition of the term to Equation (5.22) is a simplified attempt to account for the fact that
UL is, in fact, not independent of temperature. In fact, the temperature dependence of
UL
is quite complex. The attempt here is to utilize available test data by using a curve fitting technique. Figure 5.8 shows typical values and trends for these two concentrators.

Figure 5.8 Collector efficiency for a typical parabolic trough and a typical parabolic dish collector.
The largest source of error arises from the fact that, in using a simple
Now if the
It is noteworthy that in some of the literature, non-linearity on the
5.4.3 Parabolic Dish and Central Receivers - Constant-T Models
When a collector operates at a fixed temperature, and it is designed for operation at that temperature, there is little need to determine its performance under varying temperature operating conditions. Parabolic dish collectors that are part of dish/engine systems, and central receiver systems are usually in this category.
If operated at a constant temperature, and that temperature is significantly higher than ambient temperature, the rate of heat loss term in Equation
(5.9) is a constant, and the useful energy out is optical energy collected minus this constant. The result is a thermal output linearly proportional to solar irradiance once a minimum ‘threshold’ solar irradiance level has been reached. This simple behavior is pictured in Figure 4.8 d).
(5.25)
The only variable unaccounted for here, is the variation in the overall heat loss coefficient, UL caused by variations in wind velocity and direction. For parabolic dishes using cavity receivers, UL will also change with the tilt angle of the cavity relative to the earth. This angle changes as the dish tracks the sun across the sky. Data on both of these effects can be found in Stine & McDonald (1989).
Usually for these combined concentrator/engine systems, the combined collector/engine system performance is modeled. The output curve is similar to Figure (4.8d) but with the offset including both collector thermal losses, and engine losses. These will be discussed in Chapter 11.
The performance of a photovoltaic panel or concentrating photovoltaic collector is defined in terms of its efficiency as a function of load resistance and cell temperature. Equations defining the appropriate efficiency are given as Equation (5.17) for flat-plate photovoltaic panels and (5.20) for concentrating photovoltaic collectors. Normally, the efficiency of a photovoltaic panel or collector is determined based on experimental data.
A curve of efficiency as a function of voltage across the panel at different levels of irradiance is shown in Figure 5.9. This curve is derived from the basic I-V data shown in Figure 5.4 and is for a cell temperature of 25oC, air mass = 1.5.
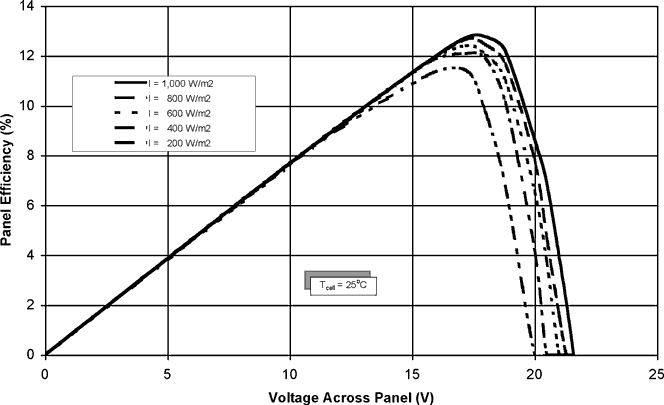
Figure 5.9 Photovoltaic panel efficiency at different levels of solar irradiance. Data shown are for a cell temperature of 25 oC and an air mass of 1.5.
The peak power points described in Section 5.2.4 above are obvious in this plot, however we are now looking at efficiency variation rather than power variation as in Figure 5.5. It is important to note that the panel efficiency remains almost the same at all levels of insolation Although Figure 5.5 shows a marked decrease in power as solar irradiance decreases, the efficiency decreases only slightly with irradiance level.
The effect of elevated cell temperatures on panel efficiency is shown in Figure 5.10. Here we see a significant reduction in panel efficiency as cell temperature increases. The typical temperature coefficient of efficiency is between value here is -0.5 to -0.6%/oC
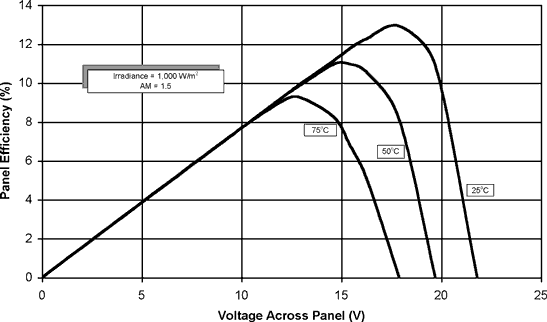
Figure 5.10 Photovoltaic panel efficiency at 1,000 W/m2 for different cell temperatures. Data shown are for an air mass of 1.5.
Model - All of the factors discussed above must be included in a photovoltaic panel or collector performance model. The performance of a photovoltaic panel is a function of the solar irradiation level, the temperature of the cell and the air mass which affects the spectral distribution of the incident irradiance as discussed in Chapter 2, section 2.2.2 and demonstrated on Figure 2.5. One such model for photovoltaic collector efficiency is
(5.26)
where: - efficiency of panel at standard irradiance, cell temperature and air
mass.
- ratio of efficiency of panel at specified irradiance level to efficiency
at standard irradiance.
- efficiency of panel at specified cell temperature to its efficiency at
the specified irradiance level.
- efficiency of panel at a specified air mass to its efficiency at
the specified irradiance level.
5.5 Measuring Collector Performance
To use a collector performance model data with some degree of confidence, it is important to understand the way in which such data are obtained and what limitations this might impose on how the data can be used. Below we describe the three most common methods of measuring collector performance. There are collector test standards available that specify both the experimental setup and the testing procedure. The most commonly accepted standards are listed in the References and Bibliography at the end of this chapter.
Testing is performed only on clear days when the solar irradiance level is high and constant. Prior to taking measurements, hot heat-transfer fluid is circulated through the absorber or receiver to bring it up to the test temperature. For a flat-plate collector, the test flow rate is generally specified by the test procedure in use. In the case of parabolic trough testing, turbulent flow is maintained within the receiver tube to ensure good heat transfer between the fluid and the wall of the receiver tube. A measurement is made only when the collector is at steady state, which is indicated by a constant rise in heat transfer fluid as it flows through the receiver.
5.5.1 Thermal Performance Measurements
In a typical test to determine solar collector efficiency, the collector aperture is aligned as close as possible to normal to the incident direct (beam) solar irradiance. This is done to eliminate any uncertainties due to off-normal incidence angle effects. Figure 5.11 is a photograph of a turntable at Sandia National Laboratory, Albuquerque used to align the aperture of a parabolic trough collector normal to the incident direct (beam) solar irradiance. Once data are obtained with the aperture normal to the sun, testing is repeated, usually only at one temperature, to determine the effect of varying angles of incidence on collector performance.

Figure 5.11
Collector module test facility at Sandia National laboratories. Courtesy of Sandia National Laboratories.Three procedures for measuring the performance of thermal collectors are used, depending on the type of collector system being tested and the experimental apparatus available. We shall briefly describe each method; collector balance, system balance and heat loss measurement methods below. Figure 5.12 depicts the test setup used in these tests graphically.
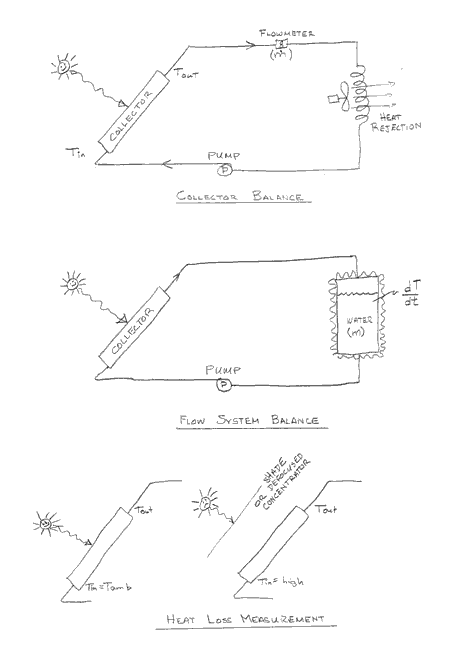
Figure 5.12 Three experimental methods for measuring collector efficiency.
Collector Balance
- The most common test method used for flat-plate and parabolic trough collectors is that depicted in Figure 5.12 a). This flow loop must incorporate accurate measurement capabilities for the fluid inlet and outlet temperatures, and the mass flow rate of the heat transfer fluid. It must also include a temperature controller connected to auxiliary heating and cooling devices so that a constant fluid inlet temperature can be maintained. The rate of energy being transferred to the heat transfer fluid under steady state conditions is given in Equation (5.2)Single collector modules are typically used in these tests, the temperature increase across a single module, especially a parabolic trough module, can sometimes be small (e.g., 1 to 5ºC in a parabolic trough) since these modules are designed to be connected in series in applications. Therefore, extreme care must be taken in making accurate temperature rise measurements. Dudley et al. (1982) describe, in general, the test procedures developed at Sandia National Laboratories for testing parabolic trough collectors.
Flow System Balance - In some cases, it is not easy to accurately measure the fluid inlet or outlet temperatures or the mass flow rate. Instead of performing the energy balance on the collector module itself, an insulated flow loop and tank can be used as illustrated in Figure 5.12 b). The energy balance for the system using this apparatus would be:
(5.27)
where:
m
- mass of fluid in entire system (kg)
- the rate of increase of fluid in the tank (K/s)
- rate of pump work entering the insulated system (W)
For this method to work, the amount of fluid must be large enough so that the bulk temperature of the fluid (and therefore the collector fluid inlet temperature) does not increase too rapidly in order to obtain an approximate steady state temperature condition.
Heat Loss Measurement - A third method is often used on concentrating collector systems and involves two tests to obtain a single performance data point. This procedure is illustrated schematically in Figure 5.12 c). First the rate of optical energy collected defined in Equation (5.4) is measured. Operating the collector with heat transfer fluid close to ambient temperature does this. Since heat loss from the collector, as shown in Equation (5.9), is proportional to the difference between fluid and ambient temperature, there should be no heat loss when they are the same temperatures.
The second test is to operate the collector at normal operating temperatures (a heater is required) without solar input. Usually defocusing the concentrator attains this test condition. Under these conditions, heat will be lost from the receiver because of the temperature difference between it and ambient. If this test is performed at different temperatures, the non-linear relationship between heat loss and temperature difference can be determined. The rate of useful energy out of the collector at any given temperature then is:
(5.28)
As with any test method, there are a number of inaccuracies that can affect the results obtained with this test procedure. Probably the most important discrepancy is from the fact that, due to the temperature difference needed to conduct heat through the absorber wall and transfer it into the working fluid, the absorber surface will be hotter than the heat transfer fluid, under normal operating conditions. However, when heat is being lost from a defocused or shaded collector during the second test above, the absorber surface will be cooler than the heat transfer fluid. This will result in the test measurement indicating heat losses that are lower than actually occur during normal operation.
Incident Angle Modifier - Most solar collector testing is performed using a two-axis tracking device that places the collector aperture normal to the sun such as shown in Figure 5.11. In actual installations, flat-plate collectors are usually mounted in a fixed position with the sun making different incident angles to the collector aperture over the day as described in Section 4.1.1.
Parabolic troughs likewise usually track about a single axis and have incident angles as described in Section 4.1.2. A non-zero angle of incidence not only changes the amount of irradiation incident on the collector aperture (already accounted for in the definitions of aperture solar irradiance), but also changes collector performance due to, among other things, variation of surface properties with incident angle and internal shading.
If total energy recovery from a collector field over a period of time is to be estimated from collector performance data, definition of the collector’s performance at other than zero incident angles is necessary. The ratio of collector efficiency at any angle of incidence, to that at normal incidence is called the ‘incident angle modifier’, Ki.
It is measured experimentally by varying the angle of incidence under noontime solar irradiance conditions with ambient temperature heat transfer fluid passing through the collector. Changes in this optical efficiency measurement give the incident angle modifier. Usually it is expressed as a polynomial curve fit as:
(5.29)
where a and b are coefficients from a polynomial curve fit.
To predict the performance of a solar collector in a system, the collector normal incidence efficiency predicted by either the linear or the non-linear ‘delta-T-over-I’ experimental data correlation model described below, is multiplied by the incident angle modifier to obtain collector efficiency:
(5.30)
Optical Efficiency - Optical efficiency, as defined in Equation (5.14) is generally determined by one of two methods. The first method, easily performed on tracking collectors, involves operating the collector at constant inlet temperature, first with the concentrator focused ‘on-sun’ and then with it ‘defocused’. The efficiency of the collector ‘on-sun’ is added to the rate of heat loss divided by the same irradiance and aperture area with the result being the optical efficiency.
This same type of test can be performed on a flat-plate collector by covering and uncovering the absorber with a sheet of opaque material.
5.5.2 Photovoltaic Performance Measurements
Due to the rapid response rate of the photovoltaic cell, testing of photovoltaic panels and concentrating photovoltaic collectors does not have many of the difficulties addressed above for thermal collectors. A detailed outline of performance testing procedures for photovoltaic panels is contained in ASTM 1036.
Generally all that is required is a variable load resistance and measurements of current through the load and voltage across the panel. A thermocouple should be placed adjacent to the photovoltaic cells to ascertain their temperature. An alternative to using a variable resistance is to connect the photovoltaic panel across a large capacitor. Taking simultaneous transient data of both voltage and current will provide the data necessary to plot an I-V curve.
Significantly more equipment is involved to determine the output at different cell temperatures and air mass.
Table 5.1 Summary of Collector Performance Models
Flat-plate Thermal Collectors:
Aperture Irradiance:
Receiver Temperature Approximation:
Performance Model:
Parabolic Troughs
Aperture Solar irradiance:
Receiver Temperature Approximation:
Performance Model:
Parabolic Dish and Central Receiver
Aperture Solar irradiance:
Receiver Temperature Approximation:
Tr = best approximation
Performance Model:
Flat-Plate Photovoltaic Panels
Aperture Irradiance:
Performance Model
Concentrating Photovoltaic Collectors
Aperture Irradiance:
Performance Model
References and Bibliography
Paitoonsurikarn, S, T. Taumoefolau and K. Lovegrove (2003) "Investigation of Natural Convection Heat Loss from a Solar Concentrator Cavity Receiver at Varying Angle of Inclination" to be presented at the 2003 ASME International Solar Energy Conference.
Stine, W. B. and C. G. McDonald (1989) "Cavity Receiver Convective Heat Loss" proceedings of the International Solar Energy Society Solar World Congress 1989 Kobe, Japan, September 4-8, 1989.
ANSI/ASHRAE Std. 93-1986 (RA 91) (1986) Methods of Testing to Determine the Thermal Performance of Solar Collectors, American Society of Heating and Refrigeration Engineers, Atlanta, GA (www.ashrae.org).
ANSI/ASHRAE Std. 95-1981 (1981) Methods of Testing to Determine the Thermal Performance of Solar Domestic Water Heating Systems, American Society of Heating and Refrigeration Engineers, Atlanta, GA (www.ashrae.org).
ANSI/ASHRAE Std. 96-1980 (RA 89) (1980) Methods of Testing to Determine the Thermal Performance of Unglazed Flat-Plate Liquid-Type Solar Collectors American Society of Heating and Refrigeration Engineers, Atlanta, GA (www.ashrae.org).
ANSI/ASHRAE Std. 109-1986 (RA 96) (1986) Methods of Testing to Determine the Thermal Performance of Flat-Plate Liquid-Type Solar Collectors Containing Boiling Liquid, American Society of Heating and Refrigeration Engineers, Atlanta, GA (www.ashrae.org).
ASTM E1036M-96e2 Standard Test Methods for Electrical Performance of Nonconcentrator Terrestrial Photovoltaic Modules and Arrays Using Reference Cells, American Society for Testing of Materials (www.astm.org)