3. The Sun’s Position
In order to understand how to collect energy from the sun, one must first be able to predict the location of the sun relative to the collection device. In this chapter we develop the necessary equations by use of a unique vector approach. This approach will be used in subsequent chapters to develop the equations for the sun’s position relative to a fixed or tracking solar collector, (Chapter 4) and the special case of a sun-tracking mirror reflecting sunlight onto a fixed point (Chapter 10). Once developed, the sun position expressions of this chapter are used to demonstrate how to determine the location of shadows and the design of simple sundials. In outline form, our development looks like this:
Although many intermediate steps of derivation used to obtain the equations described in this chapter have been omitted, it is hoped that there are adequate comments between steps to encourage the student to perform the derivation, thereby enhancing understanding of the materials presented. Brief notes on the transformation of vector coordinates are included as Section 3.5 and a summary of sign conventions for all of the angles used in this chapter is given in Table 3.3 at the end of this chapter. Figures defining each angle and an equation to calculate it are also included.
One objective in writing this chapter has been to present adequate analytical expressions so that the solar designer is able to develop simple computer algorithms for predicting relative sun and collector positions for exact design conditions and locations. This will eliminate the need to depend on charts and tables and simplified equations.
The earth revolves around the sun every 365.25 days in an elliptical orbit, with a mean earth-sun distance of 1.496 x 1011 m (92.9 x 106 miles) defined as one astronomical unit (1 AU). This plane of this orbit is called the ecliptic plane. The earth's orbit reaches a maximum distance from the sun, or aphelion, of 1.52 × 1011 m (94.4 × 106 miles) on about the third day of July. The minimum earth-sun distance, the perihelion, occurs on about January 2nd, when the earth is 1.47 × 1011 m (91.3 × 106 miles) from the sun. Figure 3.1 depicts these variations in relation to the Northern Hemisphere seasons.

Figure 3.1
The ecliptic plane showing variations in the earth-sun distance and the equinoxes and solstices. The dates and day numbers shown are for 1981 and may vary by 1 or 2 days.The earth rotates about its own polar axis, inclined to the ecliptic plane by 23.45 degrees, in approximately 24-hour cycles. The direction in which the polar axis points is fixed in space and is aligned with the North Star (Polaris) to within about 45 minutes of arc (13 mrad). The earth’s rotation about its polar axis produces our days and nights; the tilt of this axis relative to the ecliptic plane produces our seasons as the earth revolves about the sun.
We measure the passage of time by measuring the rotation of the earth about its axis. The base for time (and longitude) measurement is the meridian that passes through Greenwich, England and both poles. It is known as the Prime Meridian.
Today, the primary world time scale, Universal Time (previously called Greenwich Mean Time), is still measured at the Prime Meridian. This is a 24-hour time system, based on mean time, according to which the length of a day is 24 hours and midnight is 0 hours.
Mean time is based on the length of an average day. A mean second is l/86,400 of the average time between one complete transit of the sun, averaged over the entire year. In fact, the length of any one specific day, measured by the complete transit of the sun, can vary by up to 30 seconds during the year. The variable day length is due to four factors listed in order of decreasing importance (Jesperson and Fitz-Randolph, 1977):
Standard Time Zones - Since it is conventional to have 12:00 noon be approximately in the middle of the day regardless of the longitude, a system of time zones has been developed. See (Blaise 2000) for an interesting story about how this unification developed. These are geographic regions, approximately 15 degrees of longitude wide, centered about a meridian along which local standard time equals mean solar time. Prior to about 1880, different cities (and even train stations) had their own time standards, most based on the sun being due south at 12:00 noon.
Time is now generally measured about standard time zone meridians. These meridians are located every 15 degrees from the Prime Meridian so that local time changes in 1-hour increments from one standard time zone meridian to the next. The standard time zone meridians east of Greenwich have times later than Greenwich time, and the meridians to the west have earlier times.
Ideally, the meridians 7
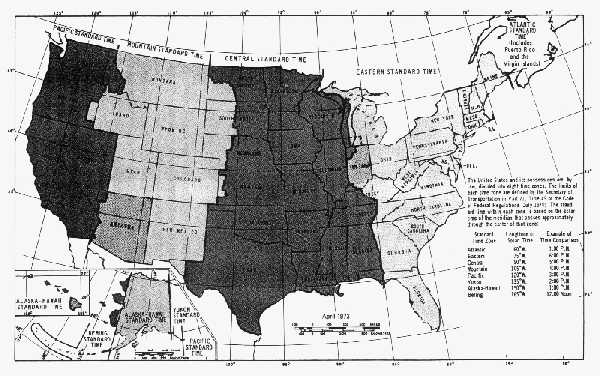
Figure 3.2
Time zone boundaries within the United States. From Jesperson and Fitz-Randolph 1977. -To complicate matters further in trying to correlate clock time with the movement of the sun, a concept known as daylight savings time was initiated in the United States in the spring of 1918 to "save fuel and promote other economies in a country at war" (Jesperson and Fitz-Randolph, 1977). According to this concept, the standard time is advanced by 1 hour, usually from 2:00 AM on the first Sunday in April until 2:00 AM on the last Sunday in October. Although various attempts have been made to apply this concept uniformly within the country, it is suggested that the designer check locally to ascertain the commitment to this concept at any specific solar site.Sidereal Time - So far, and for the remainder of this text, all reference to time is to mean time, a time system based on the assumption that a day (86,400 seconds) is the average interval between two successive times when a given point on the earth faces the sun. In astronomy or orbital mechanics, however, the concept of sidereal time is often used. This time system is based on the sidereal day, which is the length of time for the earth to make one complete rotation about its axis.
The mean day is about 4 minutes longer than the sidereal day because the earth, during the time it is making one revolution about its axis, has moved some distance in its orbit around the sun. To be exact, the sidereal day contains 23 hours, 56 minutes, and 4.09053 seconds of mean time. Since, by definition, there are 86,400 sidereal seconds in a sidereal day, the sidereal second is slightly shorter than the mean solar second is. To be specific: 1 mean second = 1.002737909 sidereal seconds. A detailed discussion of this and other time definitions is contained in another work (Anonymous, 1981, Section B).
To describe the earth's rotation about its polar axis, we use the concept of the hour angle

Figure 3.3
The hour angleSolar Time - Solar time is based on the 24-hour clock, with 12:00 as the time that the sun is exactly due south. The concept of solar time is used in predicting the direction of sunrays relative to a point on the earth. Solar time is location (longitude) dependent and is generally different from local clock time, which is defined by politically defined time zones and other approximations.
Solar time is used extensively in this text to define the rotation of the earth relative to the sun. An expression to calculate the hour angle from solar time is
where ts is the solar time in hours.
EXAMPLE
: When it is 3 hours after solar noon, solar time is 15:00 and the hour angle has a value of 45 degrees. When it is 2 hours and 20 minutes before solar noon, solar time is 9:40 and the hour angle is 325 degrees (orThe difference between solar time and local clock time can approach 2 hours at various locations and times in the United States, For most solar design purposes, clock time is of little concern, and it is appropriate to present data in terms of solar time. Some situations, however, such as energy demand correlations, system performance correlations, determination of true south, and tracking algorithms require an accurate knowledge of the difference between solar time and the local clock time.
Knowledge of solar time and Universal Time has traditionally been important to ship navigators. They would set their chronometers to an accurately adjusted tower clock visible as they left port. This was crucial for accurate navigation. At sea a ship's latitude could be easily ascertained by determining the maximum altitude angle of the sun or the altitude angle of Polaris at night. However, determining the ship’s longitude was more difficult and required that an accurate clock be carried onboard. If the correct time at Greenwich, England (or any other known location) was known, then the longitude of the ship could be found by measuring the solar time onboard the ship (through sun sightings) and subtracting from it the time at Greenwich. Since the earth rotates through 360 degrees of longitude every 24 hours, the ship then has traveled 1 degree of longitude away from the Prime Meridian (which passes through Greenwich) for every 4 minutes of time difference. An interesting story about developing accurate longitude measurements may be found in Sobel, 1999.
Equation of Time - The difference between mean solar time and true solar time on a given date is shown in Figure 3.4. This difference is called the equation of time (
EOT). Since solar time is based on the sun being due south at 12:00 noon on any specific day, the accumulated difference between mean solar time and true solar time can approach 17 minutes either ahead of or behind the mean, with an annual cycle.The level of accuracy required in determining the equation of time will depend on whether the designer is doing system performance or developing tracking equations. An approximation for calculating the equation of time in minutes is given by Woolf (1968) and is accurate to within about 30 seconds during daylight hours.
where the angle
x is defined as a function of the day number Nwith the day number, N being the number of days since January 1. Table 3.1 has been prepared as an aid in rapid determination of values of N from calendar dates.
Table 3.1 Date-to-Day Number Conversion
|
Month |
Day Number, N |
Notes |
|
January |
d |
|
|
February |
d + 31 |
|
|
March |
d + 59 |
Add 1 if leap year |
|
April |
d + 90 |
Add 1 if leap year |
|
May |
d + 120 |
Add 1 if leap year |
|
June |
d + 151 |
Add 1 if leap year |
|
July |
d + 181 |
Add 1 if leap year |
|
August |
d + 212 |
Add 1 if leap year |
|
September |
d + 243 |
Add 1 if leap year |
|
October |
d + 273 |
Add 1 if leap year |
|
November |
d + 304 |
Add 1 if leap year |
|
December |
d + 334 |
Add 1 if leap year |
|
Days of Special Solar Interest |
||
|
Solar Event |
Date |
Day Number, N |
|
Vernal equinox |
March 21 |
80 |
|
Summer solstice |
June 21 |
172 |
|
Autumnal equinox |
September 23 |
266 |
|
Winter solstice |
December 21 |
355 |
|
NOTES: |
||
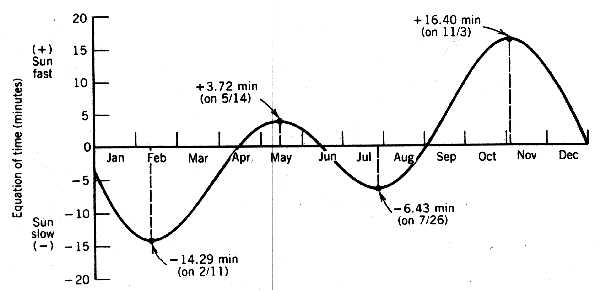
Figure 3.4
The equation of time (EOT). This is the difference between the local apparent solar time and the local mean solar time.EXAMPLE
: February 11 is the 42nd day of the year, therefore N = 42 and x is equal to 40.41 degrees, and the equation of time as calculated above isTo satisfy the control needs of concentrating collectors, a more accurate determination of the hour angle is often needed. An approximation of the equation of time claimed to have an average error of 0.63 seconds and a maximum absolute error of 2.0 seconds is presented below as Equation
(3.4) taken from Lamm (1981). The resulting value is in minutes and is positive when the apparent solar time is ahead of mean solar time and negative when the apparent solar time is behind the mean solar time:Here n is the number of days into a leap year cycle with n = 1 being January 1 of each leap year, and n =1461 corresponding to December 31 of the 4th year of the leap year cycle. The coefficients Ak and Bk are given in Table 3.2 below. Arguments for the cosine and sine functions are in degrees.
Table 3.2 Coefficients for Equation (3.4)
|
k |
Ak (hr) |
Bk (hr) |
|
0 |
2.0870 × 10-4 |
0 |
|
1 |
9.2869 × 10-3 |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Time Conversion - The conversion between solar time and clock time requires knowledge of the location, the day of the year, and the local standards to which local clocks are set. Conversion between solar time, ts and local clock time (
LCT) (in 24-hour rather than AM/ PM format) takes the formwhere EOT is the equation of time in minutes and LC is a longitude correction defined as follows:
(3.6)
and the parameter D in Equation (3.5) is equal to 1 (hour) if the location is in a region where daylight savings time is currently in effect, or zero otherwise.
EXAMPLE
: Let us find the clock time for solar noon at a location in Los Angeles, having a longitude of 118.3 degrees on February 11. Since Los Angeles is on Pacific Standard Time and not on daylight savings time on this date, the local clock time will be:
The plane that includes the earth 's equator is called the equatorial plane. If a line is drawn between the center of the earth and the sun, the angle between this line and the earth's equatorial plane is called the declination angle
As the earth continues its yearly orbit about the sun, a point is reached about 3 months later where a line from the earth to the sun lies on the equatorial plane. At this point an observer on the equator would observe that the sun was directly overhead at noontime. This condition is called an equinox since anywhere on the earth, the time during which the sun is visible (daytime) is exactly 12 hours and the time when it is not visible (nighttime) is 12 hours. There are two such conditions during a year; the autumnal equinox on about September 23, marking the start of the fall; and the vernal equinox on about March 22, marking the beginning of spring. At the equinoxes, the declination angle

Figure 3.5
The declination angleThe winter solstice occurs on about December 22 and marks the point where the equatorial plane is tilted relative to the earth-sun line such that the northern hemisphere is tilted away from the sun. We say that the noontime sun is at its "lowest point" in the sky, meaning that the declination angle is at its most negative value (i.e.,
Accurate knowledge of the declination angle is important in navigation and astronomy. Very accurate values are published annually in tabulated form in an ephemeris; an example being (Anonymous, 198l). For most solar design purposes, however, an approximation accurate to within about 1 degree is adequate. One such approximation for the declination angle is
where the argument of the cosine here is in degrees and N is the day number defined for Equation (3.3) The annual variation of the declination angle is shown in Figure 3.5.
The latitude angle
Other latitude angles of interest are the Tropic of Cancer (+23.45 degrees latitude) and the Tropic of Capricorn (- 23.45 degrees latitude). These represent the maximum tilts of the north and south poles toward the sun. The other two latitudes of interest are the Arctic circle (66.55 degrees latitude) and Antarctic circle (-66.5 degrees latitude) representing the intersection of a perpendicular to the earth-sun line when the south and north poles are at their maximum tilts toward the sun. As will be seen below, the tropics represent the highest latitudes where the sun is directly overhead at solar noon, and the Arctic and Antarctic circles, the lowest latitudes where there are 24 hours of daylight or darkness. All of these events occur at either the summer or winter solstices.
When we observe the sun from an arbitrary position on the earth, we are interested in defining the sun position relative to a coordinate system based at the point of observation, not at the center of the earth. The conventional earth-surface based coordinates are a vertical line (straight up) and a horizontal plane containing a north-south line and an east-west line. The position of the sun relative to these coordinates can be described by two angles; the solar altitude angle and the solar zenith angle defined below. Since the sun appears not as a point in the sky, but as a disc of finite size, all angles discussed in the following sections are measured to the center of that disc, that is, relative to the "central ray" from the sun.
3.2.1 Solar Altitude, Zenith, and Azimuth Angles
The solar altitude angle
The other angle defining the position of the sun is the solar azimuth angle (A). It is the angle, measured clockwise on the horizontal plane, from the north-pointing coordinate axis to the projection of the sun’s central ray.
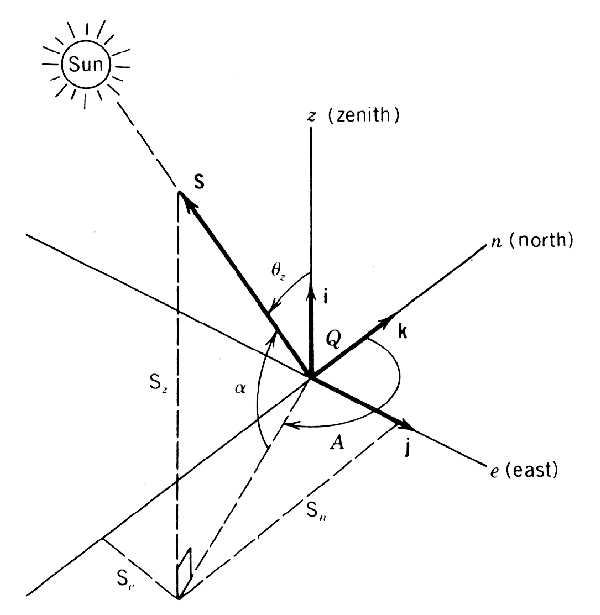
Figure 3.6
Earth surface coordinate system for observer at Q showing the solar azimuth angle Α, the solar altitude angleThe reader should be warned that there are other conventions for the solar azimuth angle in use in the solar literature. One of the more common conventions is to measure the azimuth angle from the south-pointing coordinate rather than from the north-pointing coordinate. Another is to consider the counterclockwise direction positive rather than clockwise. The information in Table 3.3 at the end of this chapter will be an aid in recognizing these differences when necessary.
It is of the greatest importance in solar energy systems design, to be able to calculate the solar altitude and azimuth angles at any time for any location on the earth. This can be done using the three angles defined in Section 3.1 above; latitude
For this derivation, we will define a sun-pointing vector at the surface of the earth and then mathematically translate it to the center of the earth with a different coordinate system. Using Figure 3.6 as a guide, define a unit direction vector
S pointing toward the sun from the observer location Q:
where i, j, and k are unit vectors along the z, e, and n axes respectively. The direction cosines of S relative to the z, e, and n axes are Sz, Se and Sn, respectively. These may be written in terms of solar altitude and azimuth as
Similarly, a direction vector pointing to the sun can be described at the center of the earth
as shown inFigure 3.7. If the origin of a new set of coordinates is defined at the earth’s center, the
m axis can be a line from the origin intersecting the equator at the point where the meridian of the observer at Q crosses. The e axis is perpendicular to the m axis and is also in the equatorial plane. The third orthogonal axis p may then be aligned with the earth’s axis of rotation. A new direction vector S´ pointing to the sun may be described in terms of its direction cosines S´m , S'e and S'p relative to the m, e, and p axes, respectively. Writing these in terms of the declination and hour angles, we have
(3.11)
Note that
S´e is negative in the quadrant shown in Figure 3.7.
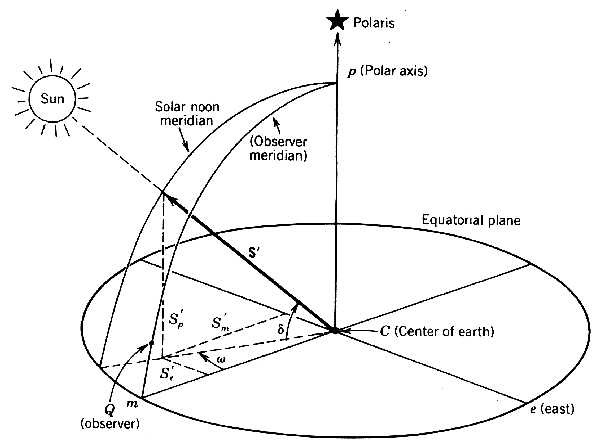
Figure 3.7
Earth center coordinate system for the sun ray direction vector S defined in terms of hour angleThese two sets of coordinates are interrelated by a rotation about the
e axis through the latitude angle
(3.12)
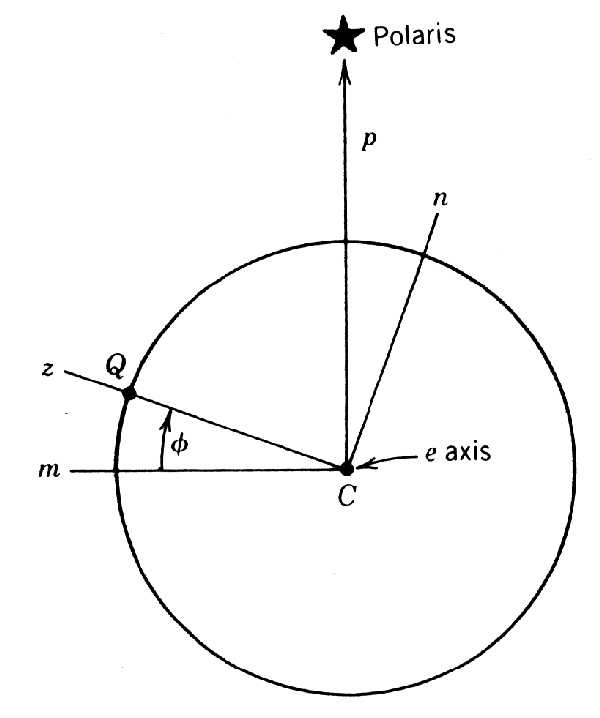
Figure 3.8
Earth surface coordinates after translation from the observer at Q to the earth center C.
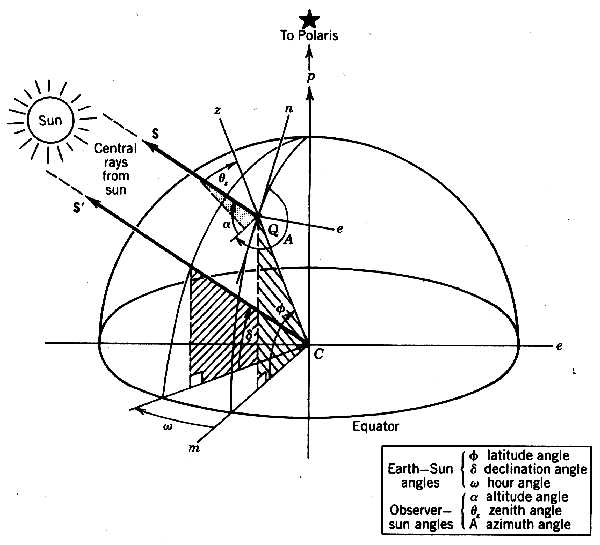
Figure 3.9
Composite view of Figures 3.6, 3.7 and 3.8 showing parallel sun ray vectors S and S’ relative to the earth surface and the earth center coordinates.Solving, we have
(3.13)
Substituting Equations (3.10) and (3.1)(3.11) for the direction cosine gives us our three important results
Equation (3.14) is an expression for the solar altitude angle in terms of the observer’s latitude (location), the hour angle (time), and the sun’s declination (date). Solving for the solar altitude angle , we have
Two equivalent expressions result for the solar azimuth angle (A) from either Equation (3.15) or (3.16). To reduce the number of variables, we could substitute Equation (3.14) into either Equation (3.15) or (3.16); however, this substitution results in additional terms and is often omitted to enhance computational speed in computer codes.
The solar azimuth angle can be in any of the four trigonometric quadrants depending on location, time of day, and the season. Since the arc sine and arc cosine functions have two possible quadrants for their result, both Equations (3.15) and (3.16) require a test to ascertain the proper quadrant. No such test is required for the solar altitude angle, since this angle exists in only one quadrant.
The appropriate procedure for solving Equation (3.15) is to test the result to determine whether the time is before or after solar noon. For Equation (3.15), a test must be made to determine whether the solar azimuth is north or south of the east-west line.
Two methods for calculating the solar azimuth (A), including the appropriate tests, are given by the following equations. Again, these are written for the azimuth angle sign convention used in this text, that is, that the solar azimuth angle is measured from due north in a clockwise direction, as with compass directions. Solving Equation (3.15) the untested result, A’ then becomes
A graphical description of this test will follow in the next section.
Solving Equation (3.16), the untested result, A" becomes
In summary, we now have equations for both the sun’s altitude angle and azimuth angle written in terms of the latitude, declination and hour angles. This now permits us to calculate the sun’s position in the sky, as a function of date, time and location (N, ,
).
EXAMPLE:
For a site in Miami, Florida (25 degrees, 48 minutes north latitude/ 80 degrees, 16 minutes west longitude) at 10:00 AM solar time on August 1 (not a leap year), find the sun's altitude, zenith and azimuth angles.....For these conditions, the declination angle is calculated to be 17.90 degrees, the hour angle -30 degrees and the sun's altitude angle is then 61.13 degrees, the zenith angle 28.87 degrees and the azimuth angle 99.77 degrees.3.2.2 A Geometric View of Sun’s Path
The path of the sun across the sky can be viewed as being on a disc displaced from the observer. This "geometric" view of the sun's path can be helpful in visualizing sun movements and in deriving expressions for testing the sun angles as needed for Equation (3.18) to ascertain whether the sun is in the northern sky.
The sun may be viewed as traveling about a disc having a radius R at a constant rate of 15 degrees per hour. As shown in Figure 3.10, the center of this disc appears at different seasonal locations along the polar axis, which passes through the observer at Q and is inclined to the horizon by the latitude angle pointing toward the North Star (Polaris).
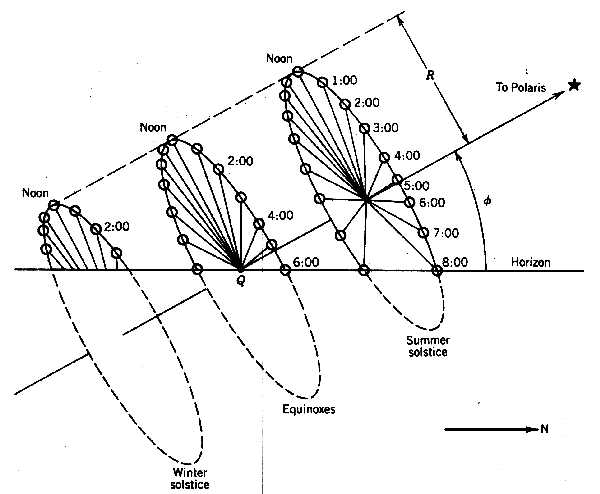
Figure 3.10
A geometric view of the sun’s path as seen by an observer at Q. Each disc has radius R.The center of the disc is coincident with the observer Q at the equinoxes and is displaced from the observer by a distance of
At the equinoxes, the sun rises exactly due east at exactly 6:00 AM (solar time) and appears to the observer to travel at a constant rate across the sky along a path inclined from the vertical by the local latitude angle. Exactly one-half of the disc is above the horizon, giving the day length as 12 hours. At noon, the observer notes that the solar zenith angle is the same as the local latitude. The sun sets at exactly 6:00 PM, at a solar azimuth angle of exactly 270 degrees or due west.
In the summer, the center of the disc is above the observer, giving rise to more hours of daylight and higher solar altitude angles, with the sun appearing in the northern part of the sky in the mornings and afternoons.
Since the inclination of the polar axis varies with latitude it can be visualized that there are some latitudes where the summer solstice disc is completely above the horizon surface. It can be shown that this occurs for latitudes greater than 66.55 degrees, that is, above the Arctic Circle. At the equator, the polar axis is horizontal and exactly half of any disc appears above the horizon surface, which means that the length of day and night is 12 hours throughout the year.
A test to determine whether the sun is in the northern part of the sky may be developed by use of this geometry. Figure 3.11 is a side view of the sun’s disc looking from the east.
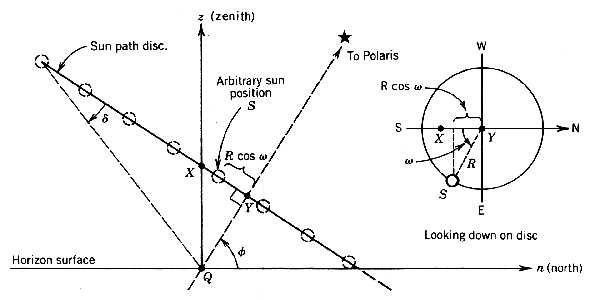
Figure 3.11
Side view of sun path disc during the summer when the disc center Y is above the observer at Q.In the summer the sun path disc of radius
R has its center Y displaced above the observer Q. Point X is defined by a perpendicular from Q. In the n - z plane, the projection of the position S onto the line containing X and Y will beThe distance XY can be found by geometry arguments. Substituting into Equation (3.20), we have
(3.21)
This is the test applied to Equation (3.18) to ensure that computed solar azimuth angles are in the proper quadrant.
3.2.3 Daily and Seasonal Events
Often the solar designer will want to predict the time and location of sunrise and sunset, the length of day, and the maximum solar altitude. Expressions for these are easily obtained by substitutions into expressions developed in Section 3.2. l.
The hour angle for sunset (and sunrise) may be obtained from Equation (3.17) by substituting the condition that the solar altitude at sunset equals the angle to the horizon. If the local horizon is flat, the solar altitude is zero at sunset and the hour angle at sunset becomes
(3.22)
The above two tests relate only to latitudes beyond ±
66.55 degrees, i.e. above the Arctic Circle or below the Antarctic Circle.
If the hour angle at sunset is known, this may be substituted into Equation (3.18) or (3.19) to ascertain the solar azimuth at sunrise or sunset.
The hours of daylight, sometimes of interest to the solar designer, may be calculated as
(3.23)
where ωs is in degrees. It is of interest to note here that although the hours of daylight vary from month to month except at the equator (where ), there are always 4,380 hours of daylight in a year (non leap year) at any location on the earth.
Another limit that may be obtained is the maximum and minimum noontime solar altitude angle. Substitution of a value of into Equation (3.17) gives
where denotes the absolute value of this difference. An interpretation of Equation (3.24) shows that at solar noon, the solar zenith angle (the complement of the solar altitude angle) is equal to the latitude angle at the equinoxes and varies by ±23.45 degrees from summer solstice to winter solstice.
EXAMPLE: At a latitude of 35 degrees on the summer solstice (June 21), find the solar time of sunrise and sunset, the hours of daylight, the maximum solar altitude and the compass direction of the sun at sunrise and sunset.....On the summer solstice, the declination angle is +23.45 degrees, giving an hour angle at sunset of 107.68 degrees. Therefore, the time of sunrise is 4:49:17 and of sunset, 19:10:43. There are 14.36 hours of daylight that day, and the sun reaches a maximum altitude angle of 78.45 degrees. The sun rises at an azimuth angle of 60.94 degrees (north of east) and sets at an azimuth angle of 299.06 degrees (north of west).
Other seasonal maxima and minima may be determined by substituting the extremes of the declination angle, that is, ±23.45 degrees into the previously developed expressions, to obtain their values at the solstices. Since the solar designer is often interested in the limits of the sun’s movements, this tool can be very useful in developing estimates of system performance.
Now that we have developed the appropriate equations to define the direction of the sun on any day, any time and any location, let’s look at two applications, which are interesting, and may be of value to the solar designer.
An important use of your understanding of the sun’s position is in predicting the location of a shadow. Since sunlight travels in straight lines, the projection of an obscuring point onto the ground (or any other surface) can be described in terms of simple geometry.
Figure 3.12 shows a vertical pole on a horizontal surface. The problem here is to define the length and direction of the shadow cast by the pole. This will first be done in terms of radial coordinates and then in Cartesian coordinates.
In polar coordinates, for a pole height, OP and the shadow azimuth,
θs defined in the same manner as the previous azimuth angles i.e. relative to true north with clockwise being positive, we have for the shadow length:and for the shadow azimuth:
In terms of Cartesian coordinates as shown on Figure 3.12, with the base of the pole as the origin, north as the positive y-direction and east the positive x-direction, the equations for the coordinates of the tip of the shadow from the vertical pole OP are:
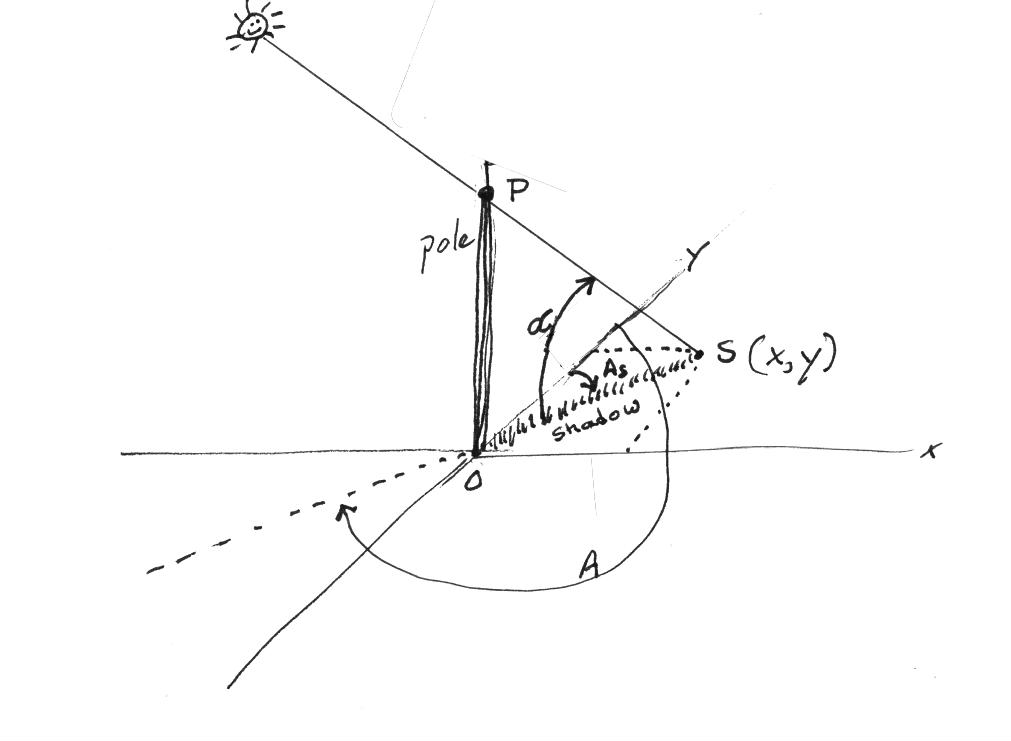
Figure 3.12 Shadow cast by pole OP showing x and y coordinates of shadow tip, and shadow azimuth
(As).Shadow coordinates are important for performing solar studies, especially related to the siting of solar energy systems. All that is needed is the latitude, hour angle and declination (i.e. the date) along with the location of the point causing the shadow. With a little bit of imagination, these equations can be used to predict shadowing of nearby terrain by trees or structures. All that is needed is to define a set of points on an object, and predict the shadow cast by that point
Example
: At a latitude of 35.7 degrees north on August 24 (day number 236) at 14:00, the sun’s altitude is 53.1 degrees and its azimuth 234.9 degrees. Then the shadow cast by a 10 cm high vertical pole is 7.51 cm long, and has a shadow azimuth (from north) of 54.9 degrees. The x- and y-coordinates of the tip of the shadow are: x = 6.14 cm and y = 4.32 cm.Throughout the history of mankind, the sun’s shadow has been used to tell he time of day. Ingenious devices casting shadows on surfaces of all shapes and orientations have been devised. However, all of these can be understood with a simple manipulation of Equations (3.25) through (3.28) developed above.
The most common sundial consists of a flat, horizontal ‘card’ with lines marked for each hour of daylight. These lines spread out from a point with the noon line pointing toward the North Pole. A ‘gnomon’ or shadow-casting device, is mounted perpendicular to the card and along the noon line. The gnomon is tapered at the local latitude angle, with its height increasing toward the north. Figure 3.13 below shows a simple horizontal sundial with the important angles defined.
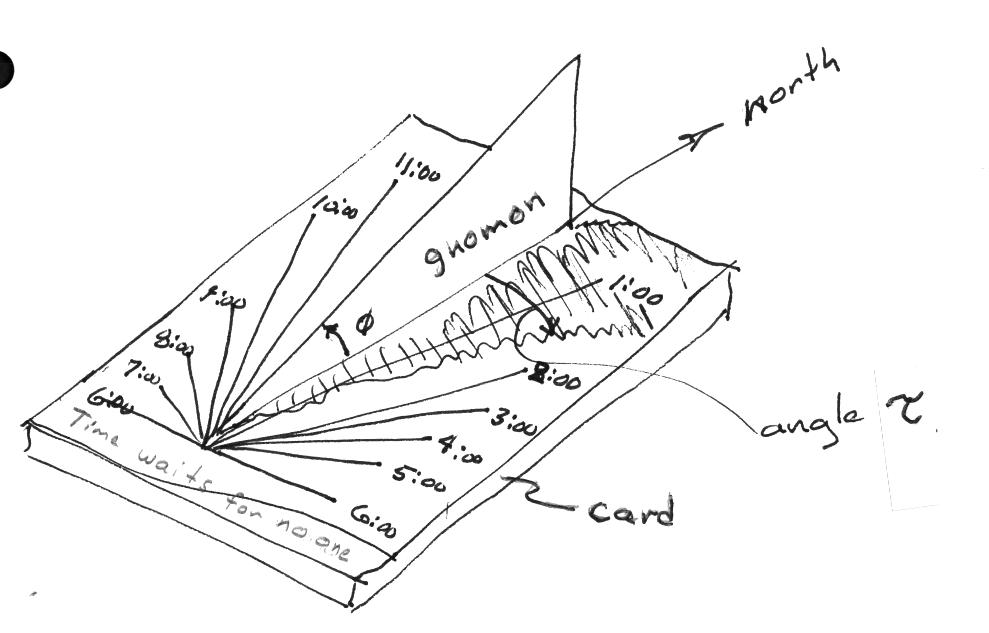
Figure 3.13
The simple horizontal sundialIn order to derive an equation for the directions of the time lines on the card, it must be assumed that the declination angle
In making a horizontal sundial, it is traditional to incorporate a wise saying about time or the sun, on the sundial card. An extensive range of sources of information about sundials, their history, design and construction is available on the internet.
3.4 Notes on the Transformation of Vector Coordinates
A procedure used often in defining the angular relationship between a surface and the sun rays is the transformation of coordinates. Defining the vector V, we obtain
where i, j, and k are unit vectors collinear with the x, y, and z-axes, respectively, and the scalar coefficients (Vx, Vy, Vz) are defined along these same axes. To describe V in terms of a new set of coordinate axes x', y ', and z' with their respective unit vectors i', j' and k' in the form
we must define new scalar coefficients . Using matrix algebra will do this. A column matrix made of the original scalar coefficients representing the vector in the original coordinate system is multiplied by a matrix which defines the angle of rotation.
The result is a new column matrix representing the vector in the new coordinate system. In matrix form this operation is represented by
(3.32)
where Aij is defined in Figure 3.14 for rotations about the x, y, or z axis.
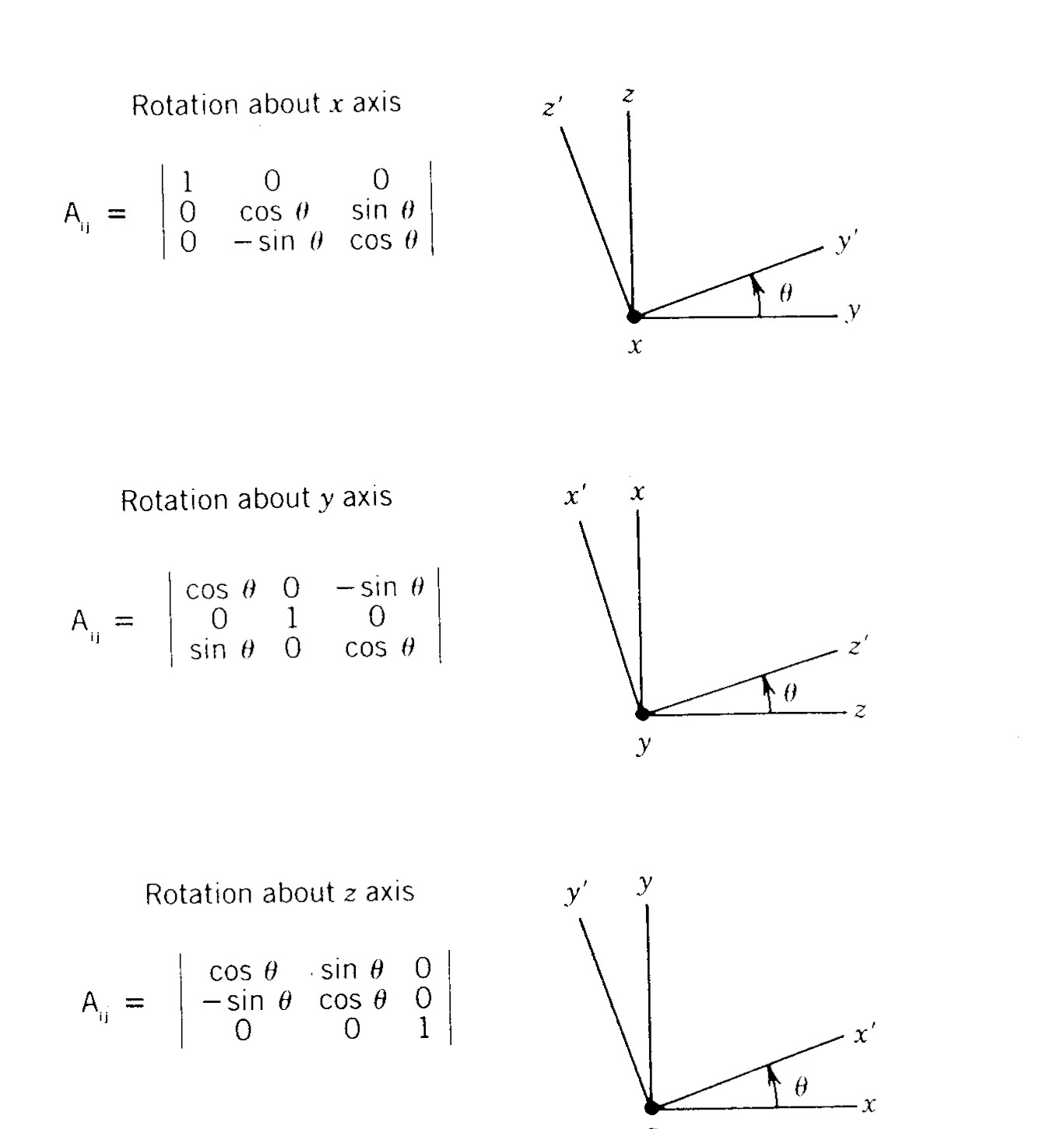
Figure 3.14 Axis rotation matrices AI j for rotation about the three principal coordinate axes by the angle .
It should be noted here that if the magnitude of V is unity, the scalar coefficients in Equations (3.30) and (3.31) are direction cosines. Note also that the matrices given in Figure 3-22 are valid only for right-handed, orthogonal coordinate systems, and when positive values of the angle of rotation, are determined by the right-hand rule.
Table 3.3 summarizes the angles described in this chapter along with their zero value orientation, range and sign convention.
Table 3.3 Sign Convention for Important Angles
| Title |
Symbol |
Zero |
Positive Direction |
Range |
Equation No. |
Figure No. |
|
Earth-Sun Angles |
||||||
|
Latitude |
|
equator |
northern hemisphere |
+/- 90o |
--- |
3.3 |
|
Declination |
|
equinox |
summer |
+/- 23.45o |
(3.7) |
3.5 |
|
Hour Angle |
|
noon |
afternoon |
+/- 180o |
(3.1) |
3.3 |
|
Observer-Sun Angles |
||||||
|
Sun Altitude |
|
horizontal |
upward |
0 to 90o |
(3.17) |
3.6 |
|
Sun Zenith |
|
vertical |
toward horizon |
0 to 90o |
(3.8) |
3.6 |
|
Sun Azimuth |
A |
due north |
clockwise* |
0 to 360o |
(3.18) or (3.19) |
3.6 |
|
Shadow and Sundial Angles |
||||||
|
Shadow Azimuth |
As |
due north |
clockwise |
0 to 360o |
(3.26) |
3.12 |
|
Gnomon Shadow |
|
noon |
afternoon |
+/- 180o |
(3.29) |
3.13 |
* looking down + axis toward origin
References and Bibliography
Anonymous (1981), "The Astronomical Almanac for the Year 1981," issued by the Nautical Almanac Office of the United States Naval Observatory.
Blaise, C. (2000), Time Lord - Sir Sandford Fleming and the Creation of Standard Time, Pantheon Books, New York.
Jesperson, J., and J. Fitz-Randolph (1977), "From Sundials to Atomic Clocks," National Bureau of Standards Monograph 155, December.
Lamm, L. 0. (1981), "A New Analytic Expression for the Equation of Time," Solar Energy 26 (5), 465.
Sobel, D. (1995), Longitude - The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time ,Fourth Estate Ltd., London.
Woolf, H. M. (1968), "On the Computation of Solar Evaluation Angles and the Determination of Sunrise and Sunset Times, "National Aeronautics and Space Administration Report NASA TM-X -164, September.
Zimmerman, J. C. (1981), "Sun Pointing Programs and Their Accuracy," Sandia National Laboratories Report SAND81-0761, September.