
2.________________________________
The sun, our singular source of renewable energy, sits at the center of the solar system and emits energy as electromagnetic radiation at an extremely large and relatively constant rate, 24 hours per day, 365 days of the year.
The rate at which this energy is emitted is equivalent to the energy coming from a furnace at a temperature of about 6,000 K (10,340ºF). If we could harvest the energy coming from just 10 hectares (25 acres) of the surface of the sun, we would have enough to supply the current energy demand of the world.
However, there are three important reasons why this cannot be done: First, the earth is displaced from the sun, and since the sun’s energy spreads out like light from a candle, only a small fraction of the energy leaving an area of the sun reaches an equal area on the earth. Second, the earth rotates about its polar axis, so that any collection device located on the earth’s surface can receive the sun’s radiant energy for only about one-half of each day. The third and least predictable factor is the condition of the thin shell of atmosphere that surrounds the earth’s surface. At best the earth’s atmosphere accounts for another 30 percent reduction in the sun’s energy. As is widely known, however, the weather conditions can stop all but a minimal amount of solar radiation from reaching the earth’s surface for many days in a row.
The rate at which solar energy reaches a unit area at the earth is called the "solar irradiance" or "insolation". The units of measure for irradiance are watts per square meter (W/m2). Solar irradiance is an instantaneous measure of rate and can vary over time. The maximum solar irradiance value is used in system design to determine the peak rate of energy input into the system. If storage is included in a system design, the designer also needs to know the variation of solar irradiance over time in order to optimize the system design.
The designer of solar energy collection systems is also interested in knowing how much solar energy has fallen on a collector over a period of time such as a day, week or year. This summation is called solar radiation or irradiation. The units of measure for solar radiation are joules per square meter (J/m2) but often watt-hours per square meter (Wh/m2) are used. As will be described below, solar radiation is simply the integration or summation of solar irradiance over a time period.
In this chapter we discuss the characteristics of the sun’s radiation first outside the earth’s atmosphere and then on the earth’s surface. We then develop analytical models that may be used by the designer to estimate the solar irradiance at a specific site.
For system design optimization studies, it is considered better to use actual recorded weather databases. Following the discussion of analytical models, we show how weather databases can be incorporated into system models such as our SIMPLES model developed in Chapter 14.
In outline form, this development is described as follows:
The system designer must know how much solar irradiance is available in order to predict the rate of energy that will be incident on a solar collector aperture. To do this, the position of the sun relative to a collector that is not parallel to the surface of the earth must be found. These techniques are developed in Chapter 3. Combining the amount of solar irradiance falling on the collector, with the orientation of the collector relative to the sun, the designer then knows the rate of solar energy being input into that collector.
2.1 Extraterrestrial Solar Radiation Characteristics
The sun, our ultimate source of energy, is just an average-sized star of average age, located in one of the spiral arms of the Milky Way galaxy as simulated in Figure 2.l. To astronomers, it is a main sequence star of spectral class G. This means that it has an apparent surface temperature around 6,000K (10,340ºF) and is of average brightness. Other known main sequence stars have luminosities up to 1,000 times greater and 1,000 times less and temperatures ranging from 3,000K (4,900ºF) to 16,000K (28,300ºF).

Figure 2.1 A galaxy (Andromeda) thought to be similar to our Milky Way galaxy in which the approximate location of where our sun would be is noted (photo courtesy of NASA).
At the center of the sun it is presumed that hydrogen nuclei are combining to form helium nuclei in a thermonuclear fusion process where the excess binding energy is released into the body of the sun. This energy is released at the rate of 3.83
× 1026 W.Most of the electromagnetic radiation reaching the earth emanates from a spherical outer shell of hot dense gas called the photosphere. When we "see" the sun, this is the "surface" we see as shown in Figure 2.2. This region has a diameter of approximately 1.39
× 109 m (864,000 miles) and appears as a bright disc with some "limb darkening" (brighter near the center) since radiation coming to us from the outer edges comes from higher and cooler layers of gas. Observations of sunspot movement indicate that the sun does not rotate uniformly. The region near its equator rotates with a period of about 27 days, whereas the polar regions rotate more slowly, with a period of about 32 days.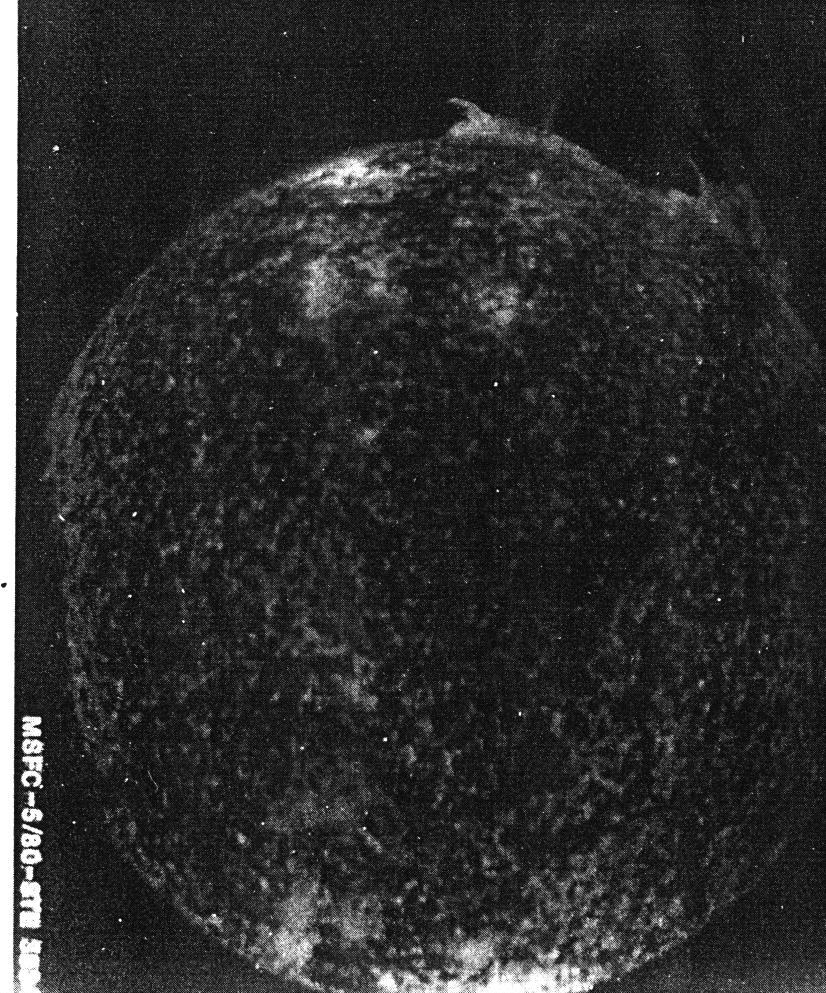
Figure 2.2 The sun as viewed from Skylab (photo courtesy of NASA).
Beyond the photosphere are the chromosphere and the corona. These regions are characterized by low-density gases, higher temperature, and timewise variations in energy and diameter. Because of the low density and thus minimal energy emission from these regions, they are of little significance to earth-based solar thermal applications. They do, however, produce uniform cyclic variations in the X-ray and ultraviolet (UV) components of the solar spectrum, having approximately 11-year periods, coincident with the sunspot cycles. Table 2.1 summarizes the important characteristics
of the sun.Table 2.1. Characteristics of the Sun
|
Present age: |
4.5 × 109 years |
|
Life expectancy: |
10 × 109 years |
|
Distance to earth: |
|
|
mean |
1.496 × 1011 m = 1.000AU |
|
variation |
1.016735 to 0.98329 AU |
|
Diameter (photosphere) |
1.39 × 109 m |
|
Angular diameter (from earth): |
9.6 × 10-3 radians |
|
Variation |
±1.7% |
|
Volume (photosphere): |
1.41 × 1027m3 |
|
Mass: |
1.987 × 1030 kg |
|
Composition: |
|
|
hydrogen |
73.46% |
|
helium |
24.85% |
|
oxygen |
0.77% |
|
carbon |
0.29% |
|
iron |
0.16% |
|
neon |
0.12% |
|
nitrogen, silicon, magnesium, sulfur, etc. |
<0.1% |
|
Density: |
|
|
mean |
14.1 kg/m3 |
|
center |
1,600 kg/m3 |
|
Solar radiation: |
|
|
entire sun |
3.83 × 1026 W |
|
unit area of surface |
6.33 × 107 W/m2 |
|
at 1 AU (i.e. the solar constant) |
1,367 W/m2 |
|
Temperature: |
|
|
center |
15,000,000 K |
|
surface (photosphere) |
6,050 K |
|
chromosphere |
4,300-50,000 K |
|
corona |
800,000-3,000,000 K |
|
Rotation: |
|
|
solar equator |
26.8 days |
|
30º latitude |
28.3 days |
|
60º latitude |
30.8 days |
|
75º latitude |
31.8 days |
|
Energy source: |
|
|
Rate of mass loss: |
4.1 ×109 kg/s |
SOURCE: Abridged from Eddy (1979).
2.1.1 The Solar Constant
The radiation intensity on the surface of the sun is approximately 6.33
× 107 W/m2. Since radiation spreads out as the distance squared, by the time it travels to the earth (1.496 × 1011 m or 1 AU is the average earth-sun distance), the radiant energy falling on 1 m2 of surface area is reduced to 1367 W as depicted in Figure 2.3.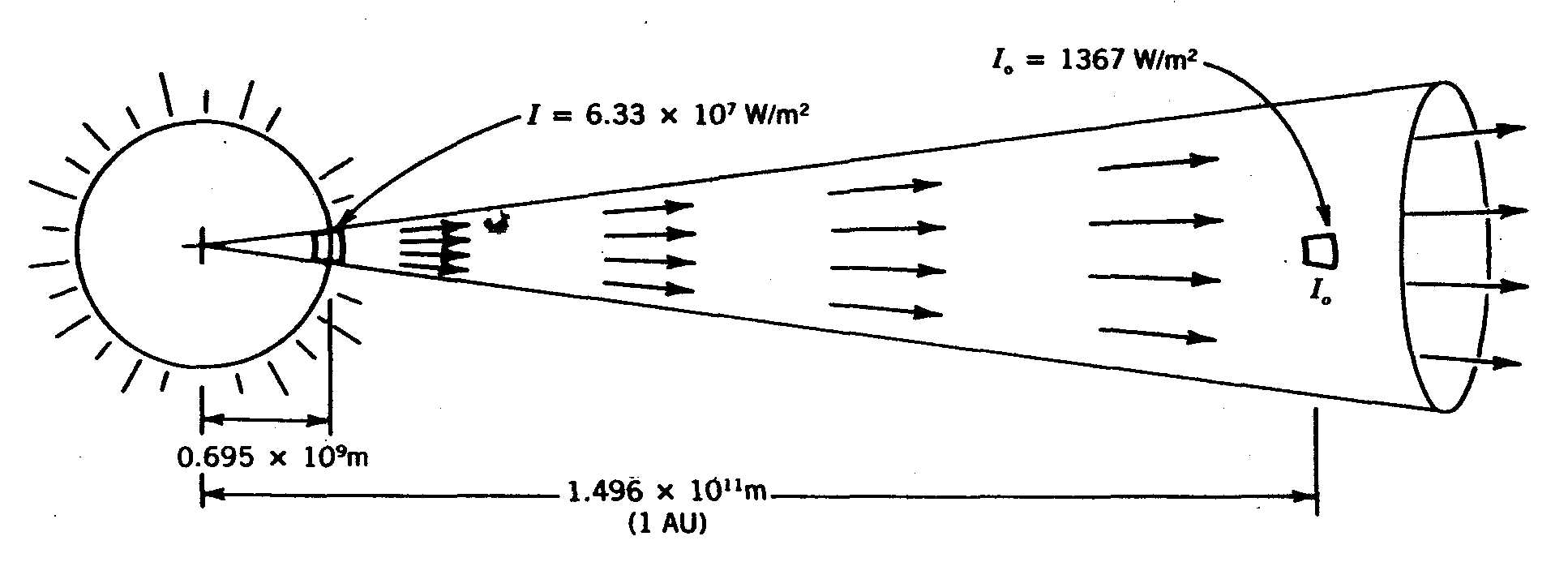
Figure 2.3 The divergence of energy from the sun to the earth.
The intensity of the radiation leaving the sun is relatively constant. Therefore, the intensity of solar radiation at a distance of 1 AU is called the solar constant Isc and has a currently accepted of 1367 W/m2 value (Fröhlich and Brusa, 1981, and Iqbal, 1983).
When converted to other units used in the solar literature, the solar constant has the values listed in Table 2.2.
Table 2.2 The Solar Constant in Units Commonly Used in Solar Literature
|
Isc = |
1367 W/m2 |
|
Isc = |
136.7 mW/cm2 |
|
Isc = |
0.1367 W/ cm2 |
|
Isc = |
1.367 x 106 erg/cm2 s |
|
Isc = |
127.0 W/ft2 |
|
Isc = |
0.03267 cal/ cm2 s |
|
Isc = |
1.960 cal/ cm2 min. |
|
Isc = |
1.960 Ly/min. (thermochemical cal/cm2 min.)a |
|
Isc = |
1.957 Ly/min. (mean cal/cm2 min.)a |
|
Isc = |
433.4 Btu/ft2 hr |
|
Isc = |
0.1204 Btu/ft2 s |
a
The langley (Ly) was originally defined in terms of the mean gram calorie rather than the more common thermochemical gram calorie. However, current literature suggests that the thermochemical calorie be used to define the langley (Delinger, 1976). The langley unit has been dropped in the SI system of units.Other values for the solar constant are found in historical literature with the value 1,353 W/m2 appearing in many publications. It is now generally believed that most of the historical discrepancies have been due to instrument calibration error (White, 1977). Recent satellite and rocket data (Duncan et al., 1982) and (Hickey et al., 1982) have confirmed that the 1,353 W/m2 value was low. Also, these data confirm that there are daily and monthly variations, believed to be not over ±0.25 percent and changes over the 11-year sunspot cycle of by about 1 percent.
Although none of these variations are of prime importance to the design of a solar energy system, studies are continuing to help explain the potential impact of these variations on our climate. It has been estimated that a drop of only 1 percent in the sun’s output of radiation would decrease the earth’s mean global temperature by more than 1ºC. The entire earth would be covered with ice if the sun’s radiation decreased by only 6 percent.
The apparent angular size of the solar disc may be calculated from the diameter of the photosphere and the earth-sun distance. At 1 AU, this is 9.3 mrad (0.553 degrees). As the earth-sun distance varies over the year, the apparent size of the sun varies by ±1.7 percent.
2.1.2 Extraterrestrial Solar Spectrum
The spectrum of the sun’s radiation just before it passes through the earth’s atmosphere is shown in Figure 2.4. Plotted along with the solar spectral irradiance for comparison is the spectral irradiance from a blackbody at 6,050 K (10,430º F). Also shown in Figure 2.4 is the integrated value of the spectral solar flux density, showing the cumulative amount of energy radiated at wavelengths between the shortest wavelength and the abscissa value. These data are based on an earlier value of the solar constant (1,353 W/m2).

Figure 2.4 Standard extraterrestrial solar spectral irradiance curve. The area under the curve is based on an earlier solar constant of 1353 W/m2 (Thekaekara, 1976).
It is interesting to note that about 45 percent of the sun’s energy comes to us at wavelengths in the visible spectrum, (nominally between 0.3 and 0.7 micrometers). Also, note that only a little more than 1 percent of the sun’s energy at shorter wavelengths (UV and X-solar radiation) and the rest (54 percent) is in the infrared (IR) region. The spectrum of the sun’s radiation changes slightly as it passes through the earth’s atmosphere, as is discussed in the following section.
Knowledge of the relative amount of energy contained in sunlight of different wavelengths permits the engineer to evaluate the impact of wavelength phenomena on total energy collection.
Example: Consider a certain collector concept that uses a glass cover on it s receiver aperture that transmits 90 percent of the sun 's energy at wavelengths below 1 micrometer and no energy at longer wavelengths. By consulting Figure 2.4 one can determine that 69.5 percent of the energy coming from the sun is coming at wavelengths shorter than 1 micrometer. A simple calculation will show that the glass receiver cover mentioned previously will pass 62.5 percent of the sun’s energy into the receiver.
For consideration of wavelength-dependent parameters (i.e., glass transmittance, surface absorptance, or photocell response) it is often visually helpful to plot these parameter versus a scale representing the percentage of energy contained in sunlight at that and shorter wavelengths. The area under this curve then represents the total percentage of energy integrated over all wavelengths. A second, nonlinear scale representing wavelength may be included, on the basis of the relationship between solar energy and wavelength shown in Figure 2.5. This is done so that wavelength dependent parameters may be presented visually.
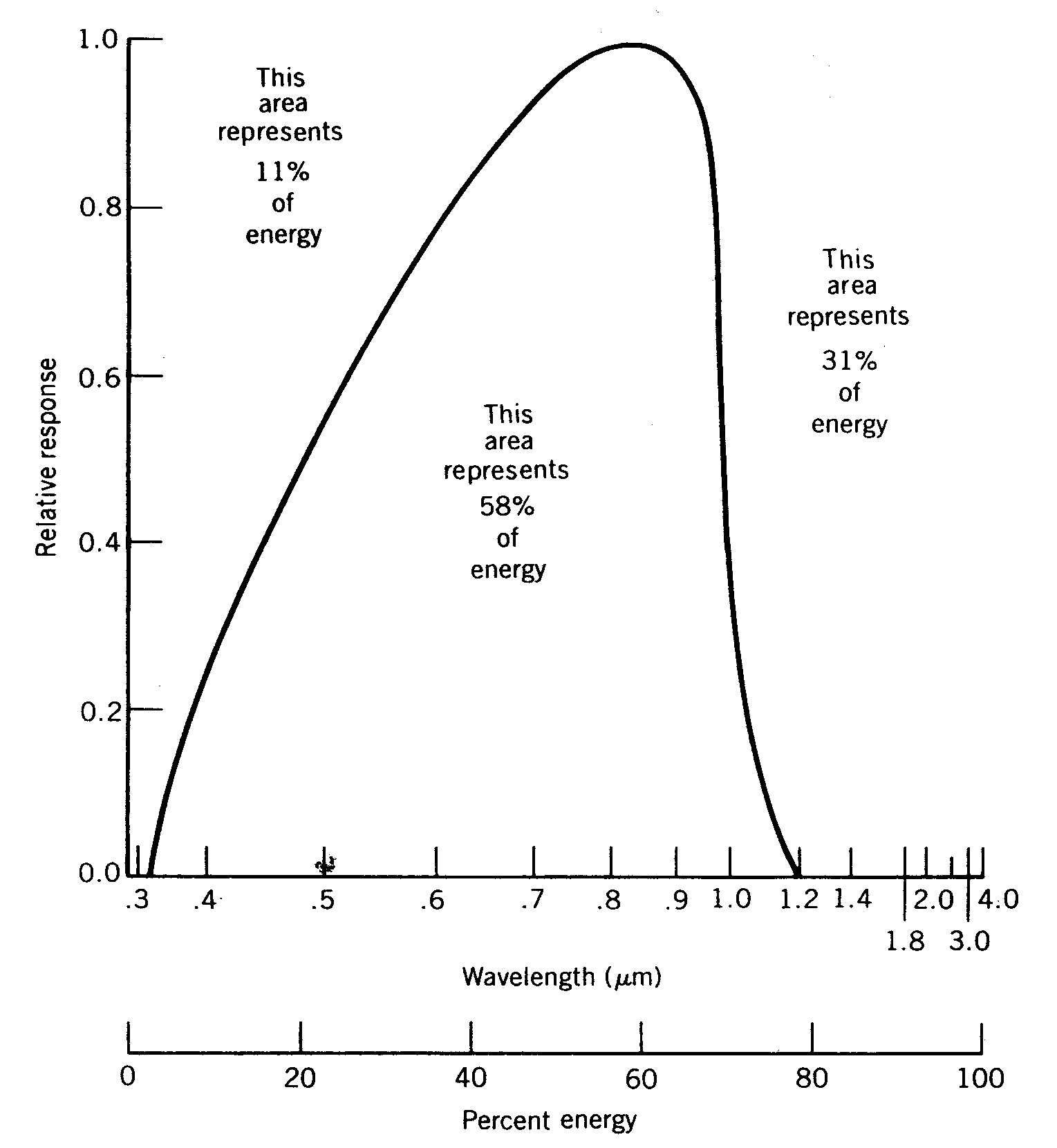
Figure 2.5
Example of a distorted wavelength scale plot. The relative spectral response of a silicon photovoltaic cell is shown, indicating that it can utilize 58 percent of the sun’s energy.Example: Figure 2.5 shows the relative response of a silicon solar cell (sometimes used to measure solar irradiance). Visually one can see that the cell responds to only 58 percent of total solar spectrum, losing 11 percent of the shorter-wavelength energy and 31 percent of the solar energy at longer wavelengths.
2.1.3 Extraterrestrial Solar Irradiance
Because the earth’s orbit is slightly elliptical, the intensity of solar radiation received outside the earth’s atmosphere varies as the square of the earth-sun distance. Solar irradiance varies by ±3.4 percent with the maximum irradiance occurring at the perihelion i.e. earth closest to the sun (January 3-5) and the minimum at the aphelion (July 5). This variation may be approximated by:
|
|
(2.1) |
where
Io is the extraterrestrial solar irradiance outside the earth’s atmosphere and N is the day number (starting at January 1).An instructional concept, and one often used in solar irradiance models, is that of the extraterrestrial solar irradiance falling on a horizontal surface. Consider a flat surface just outside the earth’s atmosphere and parallel to the earth’s surface below. When this surface faces the sun (normal to a central ray), the solar irradiance falling on it will be Io , the maximum
possible solar irradiance. If the surface is not normal to the sun, the solar irradiance falling on it will be reduced by the cosine of the angle between the surface normal and a central ray from the sun.
This concept is described pictorially in Figure 2.6. It can be seen that the rate of solar energy falling on both surfaces is the same. However, the area of surface A is greater than its projection; hypothetical surface B, making the rate of solar energy per unit area (i.e. the solar irradiance), falling on surface A less than on surface B.
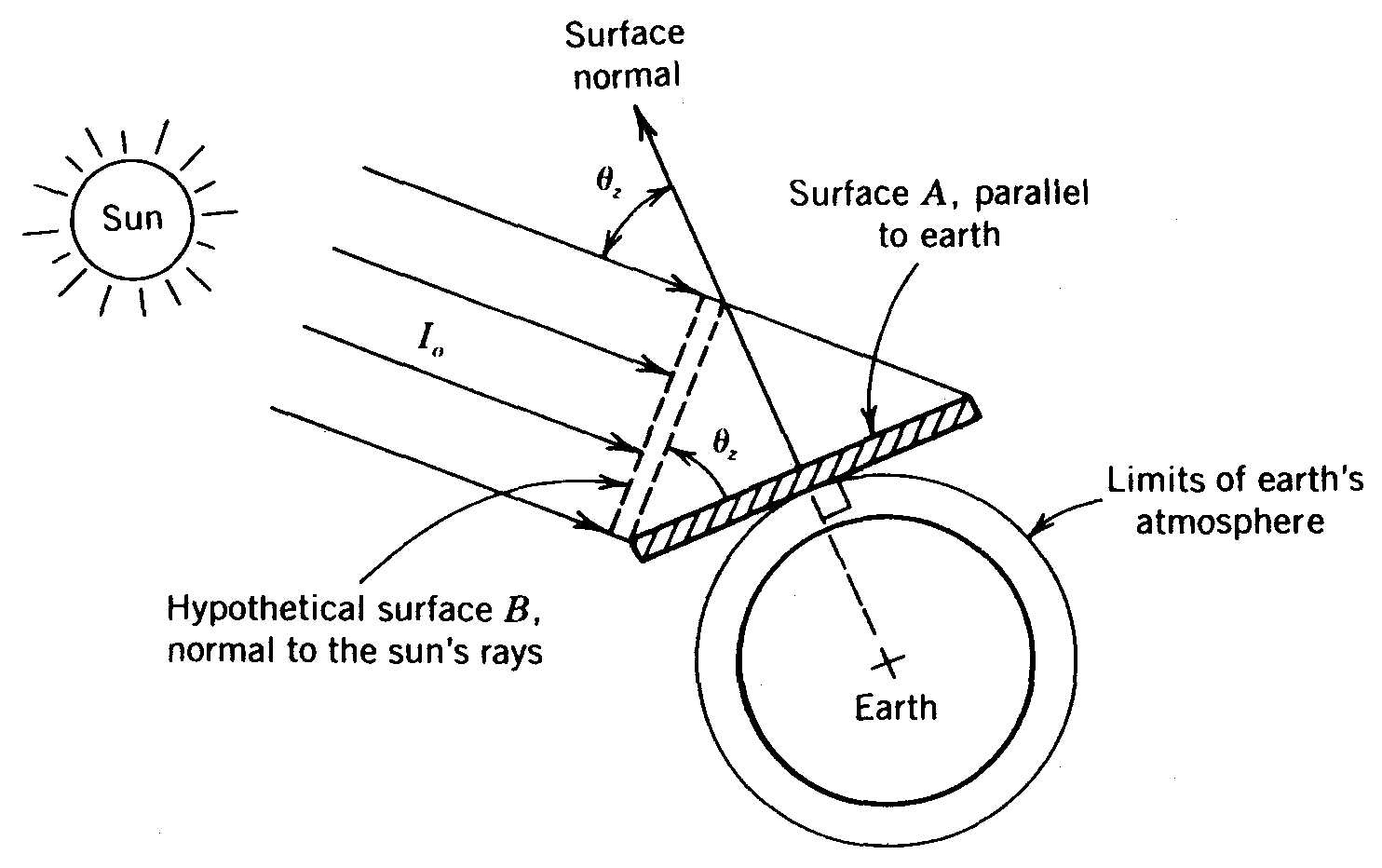
Figure 2.6
The cosine effect as it relates to the concept of extraterrestrial horizontal irradiance.The extraterrestrial solar irradiance falling on a surface parallel to the ground is
|
|
(2.2) |
where
Io is the extraterrestrial solar irradiance, andBecause of the cosine effect, the extraterrestrial solar irradiance on a horizontal varies cyclically as the earth spins on its axis. The amount of solar radiation received on a horizontal surface outside the atmosphere forms an upper limit to the amount of radiation that will fall on a horizontal surface below the earth’s atmosphere. It also describes the cosine effect without the complication of air mass and cloud cover.
Values of Io,h above a specified location on a given day at a particular time may be found from Equation
(2.2) by applying Equations (3.17) and (3.8) to determine the zenith angle and Equation (2.1) to determine the extraterrestrial radiation.2.1.4 Extraterrestrial Solar Radiation on a Surface
The total amount of energy deposited on a surface over a period of time is found by integrating (or summing) solar irradiance over that period of time. This sum is called the solar radiation and has the units of energy per unit area (J/m2 or Btu/ft2). Solar radiation is given the symbol
H in this text.Often it is of interest to determine the total amount of energy that has fallen on a surface over a full day outside the earth’s atmosphere. The daily extraterrestrial solar radiation on a horizontal surface
Ho,h may be calculated from the instantaneous values of extraterrestrial solar irradiance|
|
(2.3) |
where the time t (in seconds) is evaluated from sunrise to sunset.
Using concepts developed in Chapter 3 to describe the angle between a surface parallel to the earth and the sun, we can develop the expression below for the daily extraterrestrial solar radiation falling on a surface parallel to the earth.
The angles
Values of the daily extraterrestrial solar radiation on a horizontal surface calculated over a year at three latitudes using Equation
(2.4) are plotted in Figure 2.7. This figure shows a number of interesting points about our solar energy input. Note that the greatest amount of energy incident in one day occurs at the northernmost latitude. This high solar radiation value occurs during the summer, when the sun never sets.Also, note that at the equator, the highest solar radiation occurs in the spring and fall (at the equinoxes), not in the summer as one might expect. A summer maximum occurs only at latitudes above 23.5 degrees. The total amount of energy accumulated over a year is shown as the average solar radiation in Figure 2.7. As one might expect, the sum over a year of the daily solar radiation on a horizontal surface is highest at the equator. Surfaces in the higher (polar) latitudes lose much of the available energy as a result of the cosine effect discussed above.
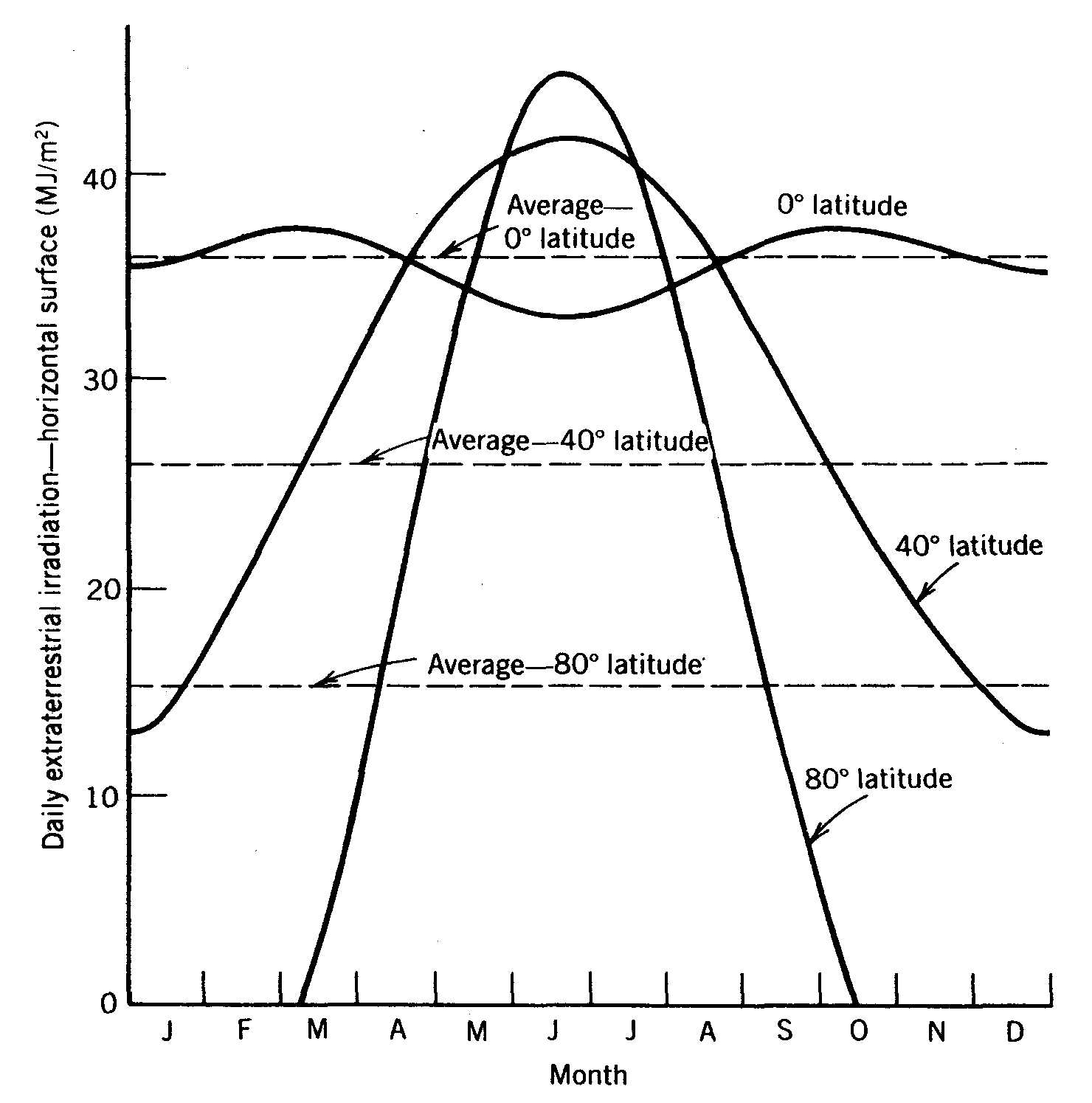
Figure 2.7
Seasonal variation of the daily extraterrestrial solar radiation (irradiation) incident on a horizontal surface outside the earth’s atmosphere in the northern hemisphere.If a surface is always pointed toward the sun (but still outside of the earth’s atmosphere), the daily extraterrestrial solar radiation on the surface will vary as shown in Figure 2.8. As latitude increases to the north, there is more energy available in the summer and less in the winter.

Figure 2.8
Seasonal variation of the daily extraterrestrial solar radiation incident on a surface always pointed normal to the sun’s rays outside the earth’s atmosphere in the northern hemisphere.The interesting result shown by Figure 2.8 is that the yearly total solar radiation on a surface maintained normal to the sun’s rays is essentially the same regardless of the latitude. This is so because anywhere on the earth there are 4,380 hours of daylight; or, taken over a year, the average length of daylight is 12 hours. Therefore, except for the slight difference caused by the winter extraterrestrial solar irradiance being about 6 percent greater than the summer solar irradiance, the total yearly extraterrestrial normal solar irradiance is essentially the same anywhere on the earth.
Note also that the yearly average of the daily normal solar radiation values is very close to the product of 12 (the average length of daylight) times the solar constant, which gives 59.1 MJ/m2. Note also, in comparing Figure 2.7 (a horizontal surface) with Figure 2.8 (a normal surface), that over the year the cosine effect reduces solar radiation on a horizontal surface by 39 percent at the equator, whereas the solar radiation is reduced by 52 percent at 40 degrees latitude and by 74 percent at 80 degrees latitude.
This understanding of extraterrestrial solar radiation on hypothetical surfaces above the earth’s atmosphere has been discussed here to give the reader some idea of the solar energy resource and the effects of the mechanics of the earth-sun system. In the section below we discuss the additional effects of the earth’s atmosphere (water vapor, carbon dioxide, clouds, smog, particulates) on the solar radiation perceived below the atmosphere.
2.2 Ground-Level Solar Radiation Characteristics
As solar radiation passes through the earth 's atmosphere, it is absorbed (the reason for some atmospheric heating), reflected (the reason astronauts can see the earth from outer space), scattered (the reason one can read this book in the shade under a tree), and transmitted directly (the reason there are shadows). At the surface of the earth, the sun has a lower intensity, a different color, and a different shape from that observed above the atmosphere.
2.2.1 Atmosphere Effects
The atmosphere causes a reduction of the extraterrestrial solar input by about 30 per cent on a very clear day to nearly 90 percent on a very cloudy day. Figure 2.9 gives an indication of the range of the absorption and scattering (forward and backward) caused by different components of the atmosphere.
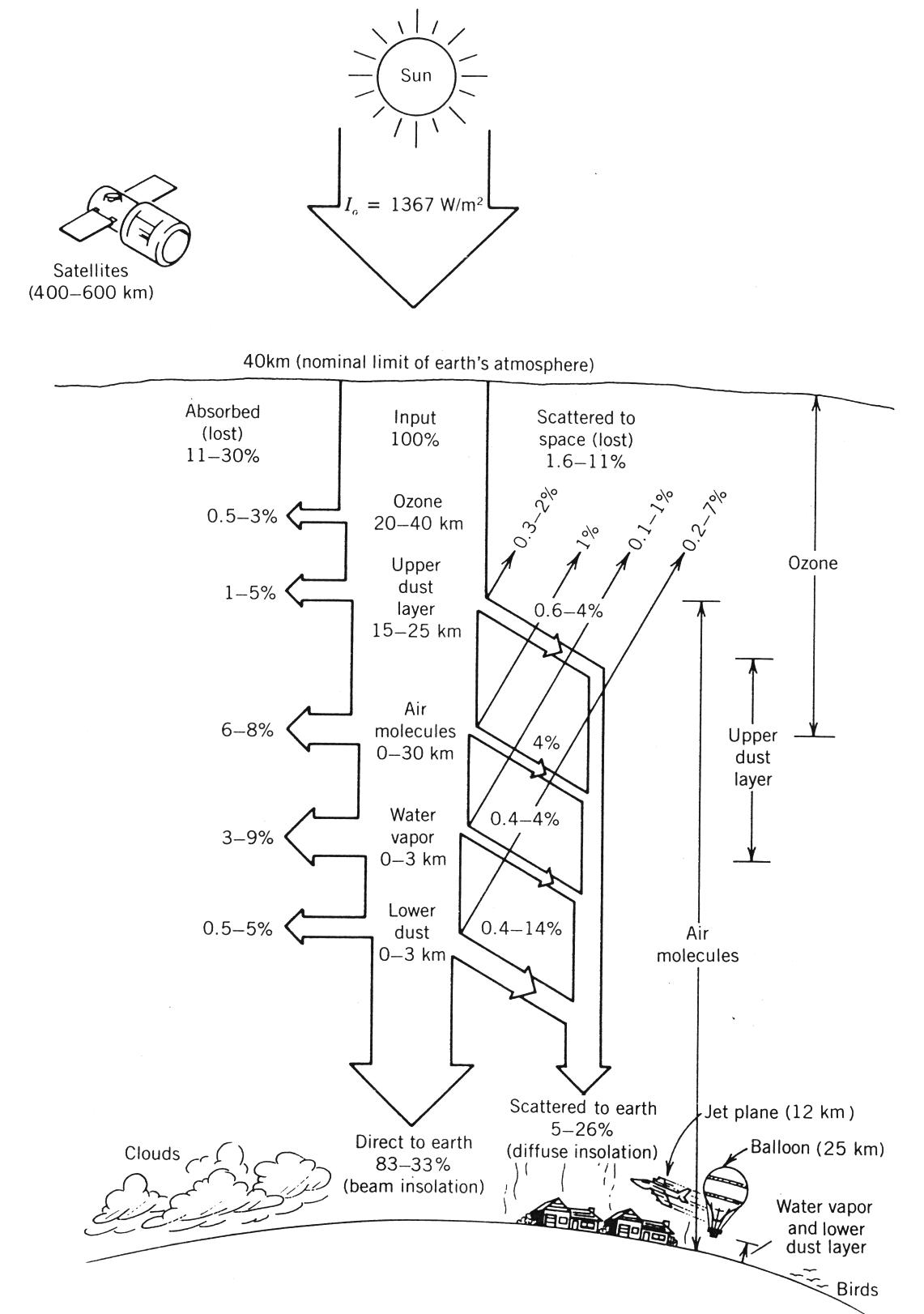
Figure 2.9 Nominal range of clear sky absorption and scattering of incident solar energy. Values are typically for one air mass (Watt, 1978).
On the surface of the earth, we perceive a beam or direct solar irradiance that comes directly from the disc of the sun and a diffuse or scattered solar irradiance that appear to come from all directions over the entire sky. In this text we will use the term direct to signify solar irradiance coming directly from the sun’s disc, and the term diffuse to indicate solar irradiance coming from all other directions. We use the traditional subscript
b to represent the direct component of solar irradiance and the subscript d to indicate the diffuse component. The sum of direct and diffuse solar irradiance is called the global or total solar irradiance and is identified by the traditional subscript t. In this book we will use the term global to indicate this sum.On a clear day, direct solar irradiance represents about 80 or 90 percent of the total amount of solar energy reaching the surface of the earth. Local blockage of the direct component of solar irradiance produces shadows. On a cloudy or foggy day when "you can’t see the sun," the direct component of solar irradiance is essentially zero and there are no shadows. The direct component of solar irradiance is of the greatest interest to designers of high-temperature solar energy systems because it can be concentrated on small areas using mirrors or lenses, whereas the diffuse component cannot.
The diffuse or scattered component of solar irradiance is what permits us to see in the shade. If there was no diffuse component of solar irradiance, the sky would appear black as at night and stars would be visible throughout the day. The first astronauts vividly described this phenomenon to us from the moon where there is no atmosphere to scatter the solar radiation.
As depicted on Figure 2.9, diffuse radiation is the result of downward scattering of solar irradiance by nitrogen, oxygen, and water molecules, water droplets, and dust particles in the atmosphere. The amount of this scattering depends on the amount of water and dust in the atmosphere and the altitude of the observer above sea level.
Since diffuse solar irradiance cannot be concentrated, only flat-plate (non-concentrating) solar collectors and some low-temperature types of concentrators (having wide acceptance angles) can collect diffuse solar irradiance. Few of the collectors used in industrial applications can utilize the diffuse component of solar radiation.
The variation of these factors, especially that of water droplets (i.e. clouds) as they attenuate the direct component and change the diffuse component, is the major unknown parameter in the design of systems to collect solar energy. Consequently, a considerable amount of effort has been and is being spent in measuring, cataloging, and developing analytical models to predict these effects.
2.2.2 Solar Spectrum
The spectrum of solar radiation has been described in Section 2.1.2. In addition to a reduction in intensity, the spectrum of solar radiation reaching the surface of the earth is also modified as it passes through the atmosphere. The processes taking place include Rayleigh and particulate (dust and water) scattering and absorption by ozone, water vapor, and carbon dioxide. All of these processes depend not only on the temporal condition of the atmosphere, but also on how much of the atmosphere the sunlight passes through.
This latter factor is measured in terms of the air mass, which is simply the ratio of the distance that solar radiation travels through the earth’s atmosphere (path length), to the distance (path length) it would travel if the sun were directly overhead.
Radiation coming from directly overhead, therefore, is said to pass through an air mass of 1.0 at sea level. Solar irradiance coming from a zenith angle of 60 degrees, would pass through approximately twice the perpendicular path length and hence an air mass of 2.0. The following expression to approximate air mass at any zenith angle
(2.5)
where the zenith angle is given in degrees. At sunset (
= 90º), this expression has a value of 37.92 and that is why there is very little solar radiation reaching the earth’s surface at sunset.
For altitudes other than sea level, the air mass calculated above is reduced by the ratio of the local atmospheric pressure to standard sea-level atmospheric pressure.
The effect on the earth’s atmosphere on the solar radiation spectrum is shown in Figure 2.10 from Thekaekara (1976) for different air masses of very clear, sea level air. Terrestrial solar spectrum data sets are available on the NREL internet site cited at the end of this chapter
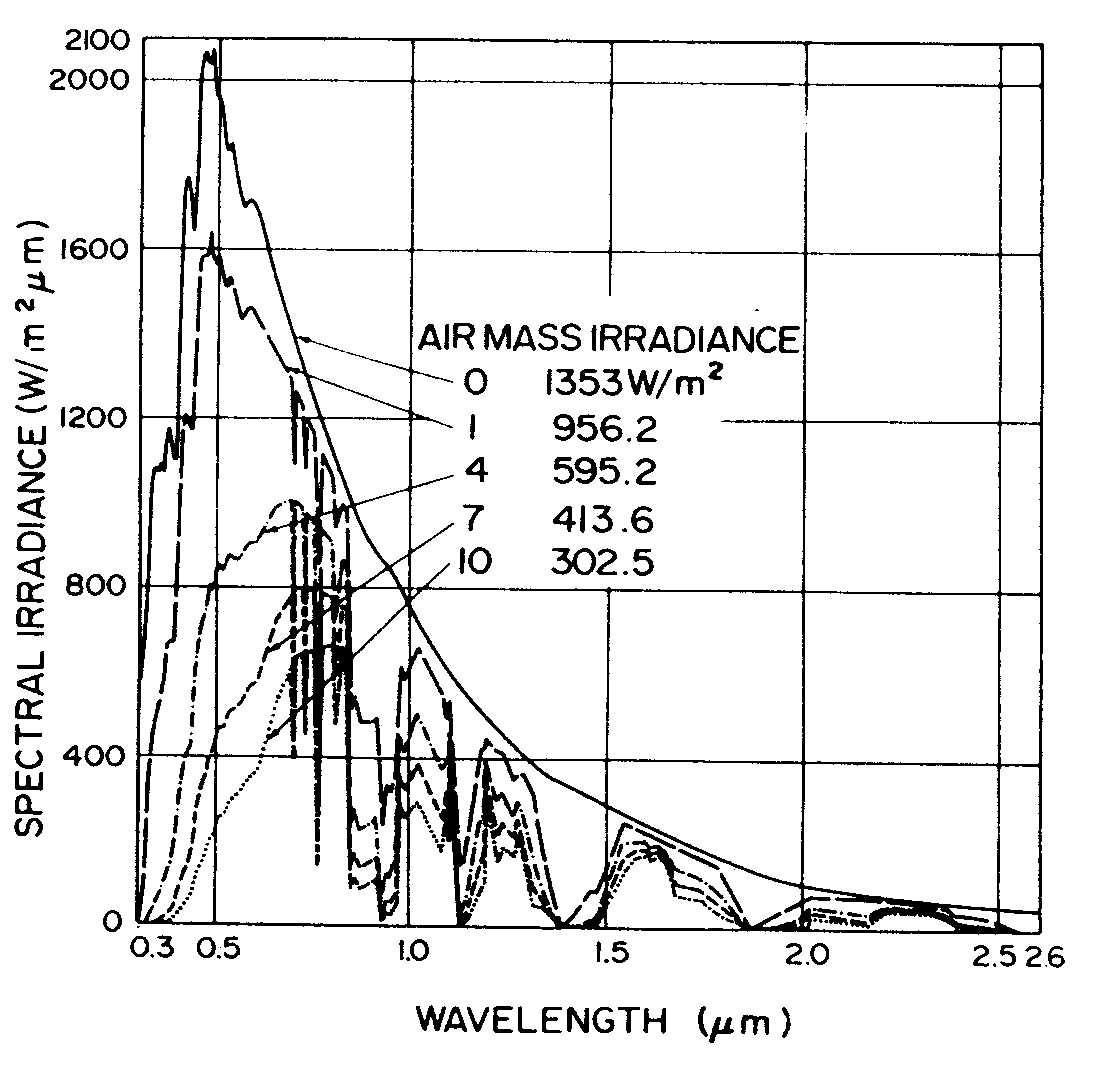
Figure 2.10
Solar spectral irradiance for different air mass values assuming the U.S. Standard atmosphere, 20 millimeters of perceptible water vapor, 3.4 millimeters of ozone, and very clear air (Thekaekara, 1976).Note in Figure 2.10 the effects of the strong water vapor and carbon dioxide absorption bands in the IR region (wavelength > 0.7 micrometers). Also note the reduction in blue and violet light (wavelength 0.3-0.4 micrometers) due to particulate and Rayleigh scattering and the reductions in the UV light (wavelength < 0.3 micrometers) due mostly to the ozone content of the upper atmosphere. This is why the sunrises and sunsets appear to be red, since the sunlight at these times must pass through more than 30 air masses. For small air mass values (in the mountains near noontime), there is an abundance of UV and short-wavelength visible light. This explains the need for strong eye and sunburn protection in the mountains and why photographs taken at high altitudes have a bluish tint.
2.2.3 Sunshape
Considering the energy coming from the direction of the sun, two factors must be considered when using highly concentrating collectors: (1) there is an intensity variation across the disc of the sun (limb darkening), and (2) the apparent radiation coming from just a few degrees away from the sun’s disc (circumsolar radiation) may have a significant energy content.
Designers of central receiver systems and solar furnaces are interested in limb darkening because the central region of the sun’s image produces a hot spot with higher flux than the overall average. The study of circumsolar radiation (caused by atmospheric scattering) has gained importance because many concentrators are designed to accept radiation coming only from the solar disc and not circumsolar radiation, thereby causing a reduction of some of the concentrator’s potential energy capture capability. The result is that even on a relatively clear day there is a difference between the radiation measured by a normal incidence pyrheliometer (discussed in the next section) having a 5-degree acceptance angle, and that which can be concentrated by a collector that accepts radiation coming only from the nominal sun’s disc (
Sunshape data are typically presented in terms of the radiance distribution
A solid angle of one steradian (sr), is defined as the solid angle that delineates an area on the surface of a reference sphere equal to the radius-squared of that sphere. There are
(2.6)
and for small values of such as the angular size of the sun from the earth
(2.7)
where must be in radians. According to this expression, if the sun’s disc subtends a cone with a vertex angle of 9.6 mrad (0.55 degrees), this is a solid angle of 7.238×10-5 sr.
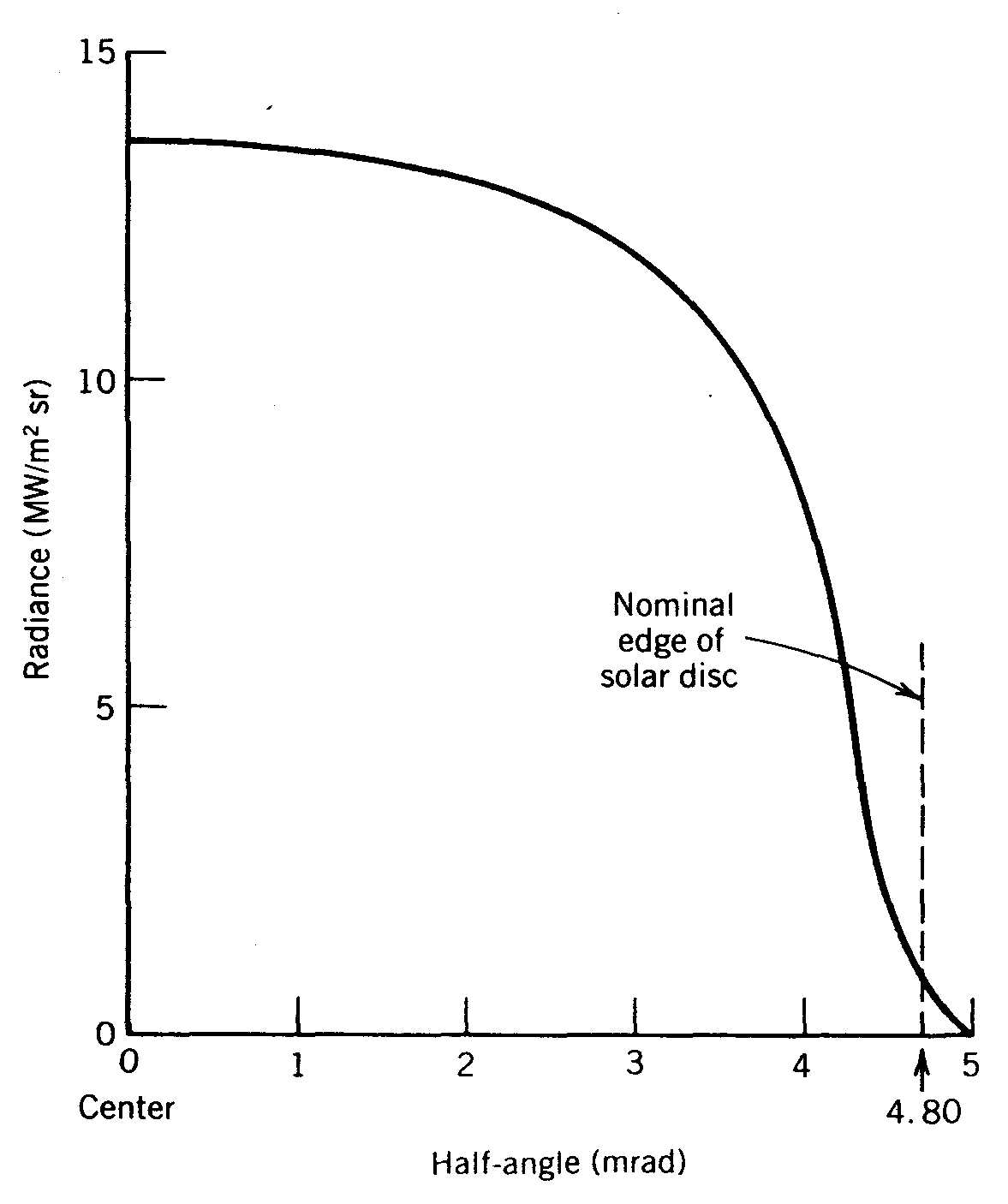
Although the circumsolar radiation varies with the condition of the atmosphere, a "standard" radiance distribution has been proposed by Bendt and Rabl (1980) and is shown in Figures 2.11 and 2.12. Figure 2.11 defines the variation of radiance across the sun’s disc, and Figure 2.12 defines the same parameter for a typical circumsolar scan. The angle is measured from the disc center and is equal to one-half of the total subtended solar disc angle
, used in subsequent chapters. The irradiance coming from a certain region is found by integrating the radiance distribution over the region of interest in the form
(2.8)
Figure 2.11
Radiance distribution of the solar disc (Bendt and Rabl, 1980).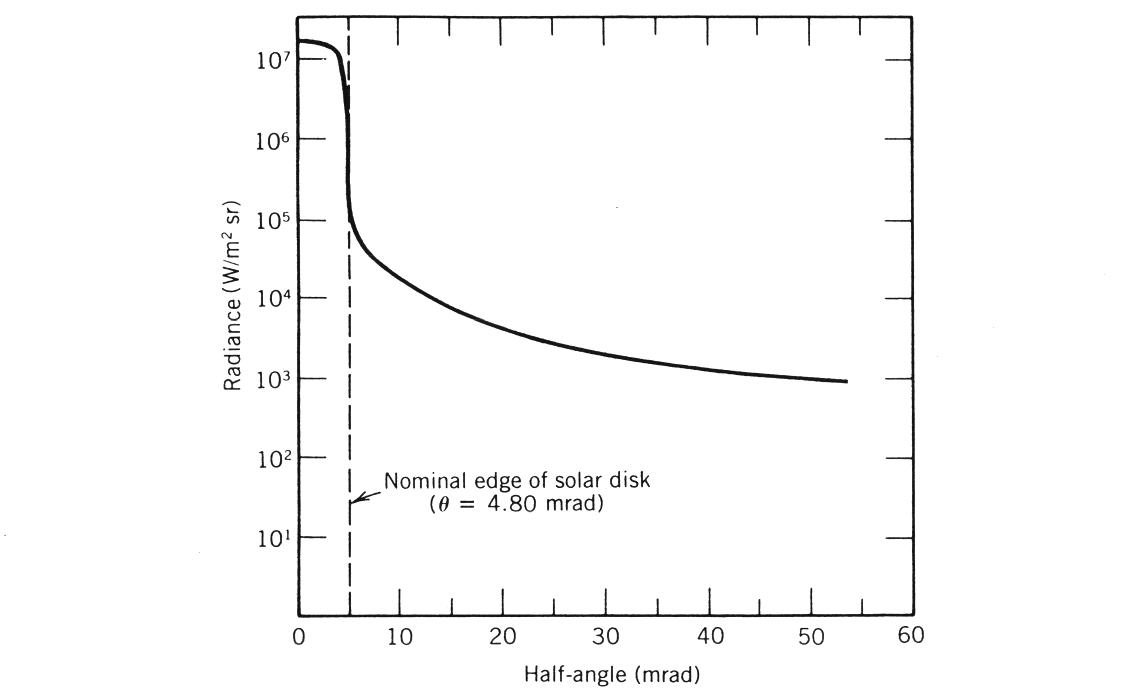
Figure 2.12
Radiance distribution of a "standard" solar scan showing both solar disc and circumsolar radiation (Bendt and Rabl, 1980).Example: If the radiance distribution is a constant 1.2×107 W/m2sr over the sun’s disc (from zero to 4.80 mrad) and there is no circumsolar radiation, then the global irradiance coming from that sunshape will be 869 W/m2.
2.3 Measurement of Solar Irradiance
2.3.1 Global Solar Irradiance - Pyranometers
The primary instrument used to measure global solar irradiance is the pyranometer, which measures the sun’s energy coming from all directions (
The most common pyranometer design uses a thermopile (multiple thermocouples connected in series) attached to a thin blackened absorbing surface shielded from convective loss and insulated against conductive losses as shown in Figure 2.13. When placed in the sun, the surface attains a temperature proportional to the amount of radiant energy falling on it. The temperature is measured and converted through accurate calibration into a readout of the global solar irradiance falling on the absorbing surface. A properly designed instrument measures radiation in all the solar wavelengths, and its response to direct radiation should be proportional to the cosine of the angle between the sun and a line normal to the pyranometer absorber surface.
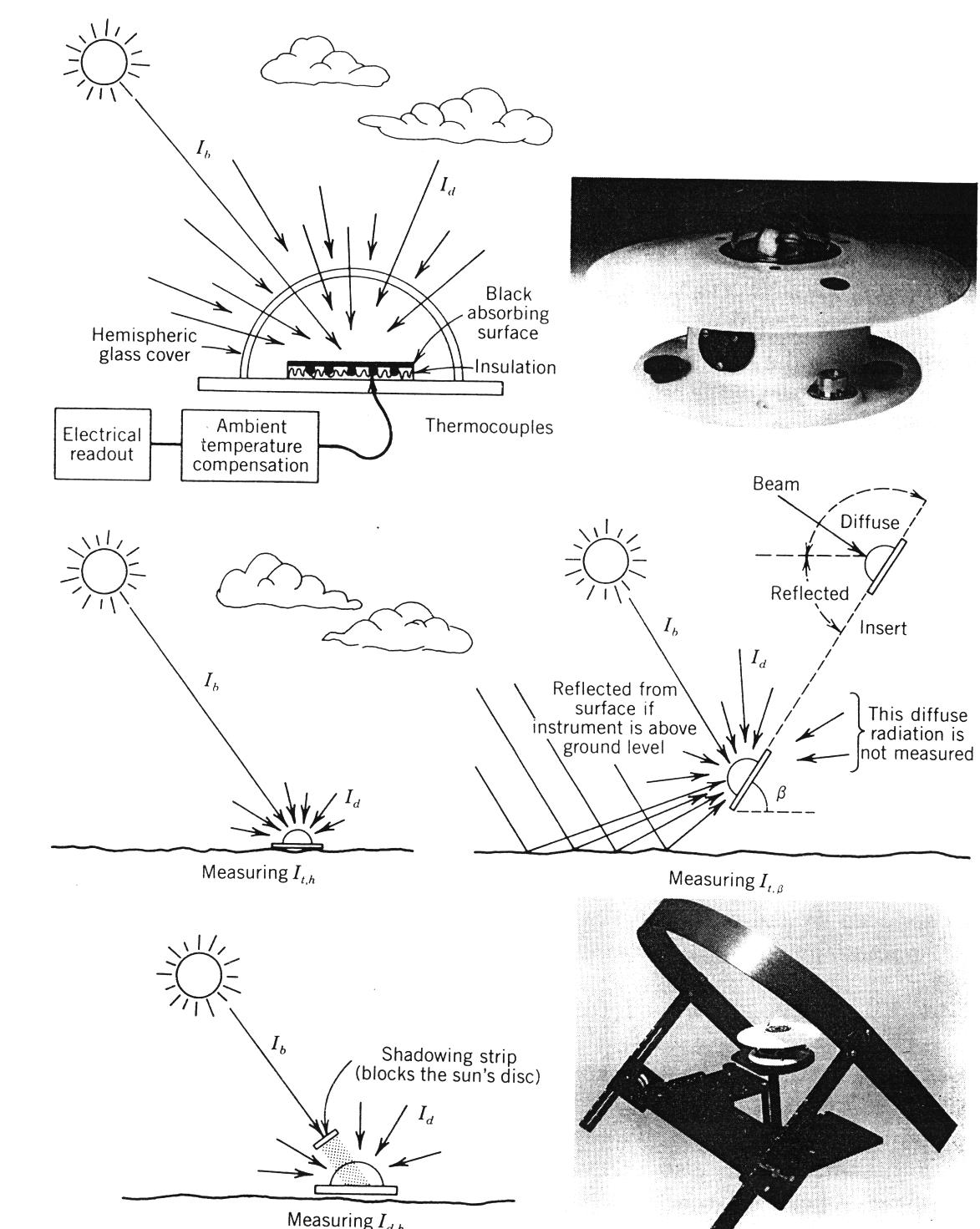
Figure 2.13
The pyranometer and its use in measuring global horizontal, tilted global, and the diffuse components of solar irradiance (photos courtesy of the Eppley Laboratory, Inc.).The typical use of a pyranometer is for measurement of the global horizontal solar irradiance. For this purpose, it is placed in a horizontal orientation and sufficiently high above the surroundings so that it has a clear, hemispheric view of the entire sky with no shading or reflecting trees or buildings within this field of view.
For a horizontally oriented pyranometer, the direct normal solar irradiance is reduced by the cosine of the angle of incidence, which in this case is the solar zenith angle
where
Ib,n represents the irradiance coming directly from the sun’s disk, measured normal to the rays and Id,h represents the diffuse radiation falling on a horizontal surface. Figure 2.14 shows typical global solar irradiance data recorded by a horizontally oriented pyranometer on both a clear and cloudy day.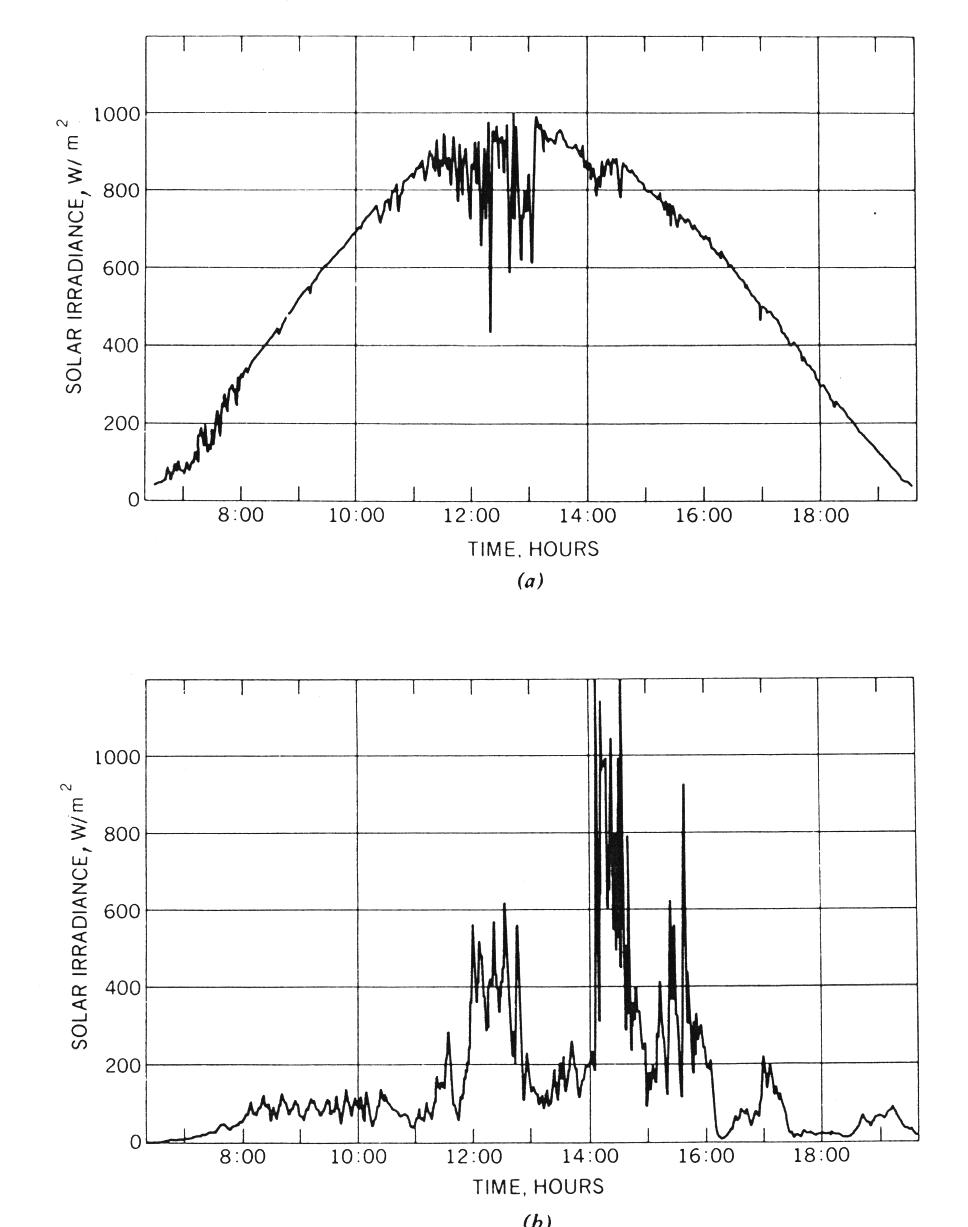
Figure 2.14
Example of global (total) irradiance on a horizontal surface for a mostly clear day and a mostly cloudy day in Greenbelt, MD (Thekaekara, 1976): (a) global solar radiation for the day was 27.1 MJ/m2; (b) global solar radiation for the day was 7.3 MJ/m2.Pyranometers may also be used to, measure the global solar irradiance on inclined surfaces. An example would be measurements from a pyranometer placed in the same plane as a tilted solar collector. As can be seen from the sketch in Figure 2.13, this measurement now includes solar energy reflected from surrounding surfaces. However, various studies have indicated the possibility that the pyranometer calibration may change with inclination. The use of this type of data, along with a model permitting the prediction of tilted global solar radiation from standard solar irradiance measurements is given in Chapter 4 of this text.
Instead of using a blackened absorbing surface with thermocouples attached (a thermopile), investigators have proposed the use of silicon photovoltaic cells as an inexpensive alternative to the thermopile. The short-circuit current produced by these cells is proportional to the intensity of radiation striking the surface. Also, the rate of response of this current to changes in solar intensity is rapid.
There are two effects that limit the accuracy of photovoltaic cell pyranometers and make them unsuitable as primary standards. These are: (1) the cosine response of the surface of a bare silicon photovoltaic cell is inaccurate, and (2) the spectral response of a solar cell is such that it is sensitive to the red and near-IR component of radiation and is insensitive to blue and violet light and the IR radiation of wavelengths longer than about 1.2 micrometers. This second characteristic was depicted graphically in Figure 2.5. In spite of these problems, relatively accurate photovoltaic pyranometers have been designed using diffusing and filtering devices to modify their input to acceptable levels of performance.
2.3.2 Direct Normal Solar Irradiance - Pyrheliometers
To measure the direct normal component of the solar irradiance only, an instrument called a normal incidence pyrheliometer or NIP is used. This device, shown in Figure 2.15 is essentially a thermopile pyranometer placed at the end of a long tube which is aimed at the sun. The aspect ratio of the tube is usually designed to accept radiation from a cone of about 5 degrees. A two-axis tracking mechanism is incorporated to maintain the sun’s disc within the acceptance cone of the instrument.
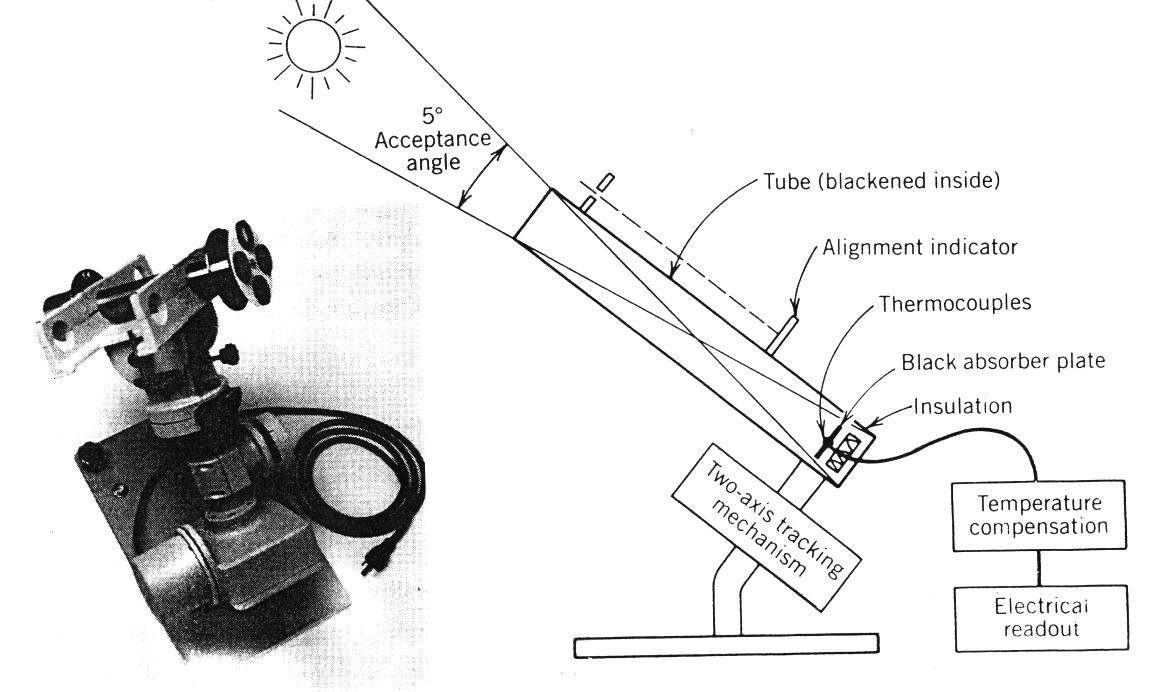
Figure 2.15
A normal incidence pyrheliometer (NIP) used for measuring the direct component of solar radiation (photo courtesy of the Eppley Laboratory, Inc.).Since the sun’s disc is approximately
2.3.3 Diffuse Irradiance
Pyranometers may be modified to measure only the diffuse component of the global horizontal radiation
Idh. Providing a "shadowing" device just large enough to block out the direct irradiance coming from the sun’s disc does this. An example of this technique is shown in Figure 2.13.To avoid moving a shadowing disc throughout the day, a shadow band is often incorporated. This band must be adjusted often during the year to keep it in the ecliptic plane. Since the shadow band blocks part of the sky, corrections for this blockage must be used.
Recently, rotating shadow band pyranometers have come into general use. With this design, the shadow band rotates slowly about the pyranometer blocking the direct irradiance from the sun every time it passes in front of the pyranometer. The signal from the pyranometer reads global horizontal irradiance most of the time, with reductions down to the diffuse irradiance level when the shadow band passes between the sun and the pyranometer. This design gives the advantage of using a single pyranometer to measure both global horizontal and diffuse horizontal solar irradiance. The rotating shadow band pyranometer also avoids the constant adjustment of the plane of the band.
The rotating shadow band pyranometer is used to determine the direct normal irradiance without the need for tracking a pyrheliometer. This is done using Equation (2.9) and calculating the solar zenith angle using techniques developed in Chapter 3.
2.3.4 Other Measurements
Sunshine Recorders
. In addition to the pyranometer and the normal incidence pyrheliometer, which measure the global and direct solar irradiance respectively, there is a traditional measurement often-reported in meteorological observations. This is the "duration of sunshine." The traditional standard instrument used to measure this parameter is the Campbell-Stokes sunshine recorder. This instrument consists of a glass sphere that focuses the direct solar radiation and burns a trace on a special pasteboard card. These recorders have been replaced in most installations by photo detector activated ‘sunshine switches.’ The data produced by these instruments are of minimal use to engineers because there is no measure of intensity other than a threshold intensity. However, attempts have been made to correlate these data with daily or monthly solar radiation levels.Cloud -cover Observations. Another source of solar irradiance data is from periodic ground observations of cloud-cover. These are made at least hourly at weather observation stations around the world. Examining the SOLMET weather data tape format discussed below will show the detail to which these observations are carried out in the United States. Cloud-cover data along with other weather data have been used to predict solar irradiance levels for the locations without solar irradiance measurement capabilities.
Satellite Observations - A similar type of measurement correlation using satellite images appears to provide accurate solar irradiance data over a wide region to a resolution of about 10 km. Promising results have been obtained with the use of satellite images made half-hourly in the visible (0.55-0.75 micrometer) and IR (9-12 micrometer) regions of the spectrum (Diak et al., 1982). Cano et. al. (1986) describe a general method for determining global solar radiation from meteorological satellite data.
More recent efforts to accurately predict solar irradiance from ground reflectance (albedo) data are described in Ineichen & Prerz (1999). They have developed and validated models for producing reliable solar irradiance data from satellite images. They developed a model that directly relates an elevation dependent clearness index to the cloud index. This methodology presents a definite advantage because it can be generalized to address the clearness index of other solar radiation components, besides global irradiance, such as direct solar irradiance.
2.4 Solar Radiation Data Bases
When designing a solar energy system, the best way to predict its energy-production performance would be to know what the minute-by-minute solar irradiance levels will be, over the lifetime of the system, and at the exact location where the system will be built. Since weather patterns are somewhat random in time and place, and are extremely difficult to predict, the system designer is forced to accept historical data, recorded at a different location, with values reconstructed from incomplete data records. Because of the inherent variability of future solar irradiance, however, historical records are an extremely useful analytical tool, appropriate for a wide range of applications. However, the designer must not be deluded to believe that system performance predicted using even the best historical data, will represent the future output of the system.
2.4.1 Typical Meteorological Year Data Sets - TMY2
In order to rectify some of these problems, typical meteorological year or TMY data sets have been developed. A typical meteorological year data set is made up from historical weather observations for a set of 12 ‘typical’ months, at a specific location. Each typical month is chosen from a multi-year set of data for a specific month, and selected because of having the ‘average’ solar radiation for that month.
For example, solar radiation data for January of maybe 30 different years is searched to determine in which year the January was typical or average. Next, 30 different February data sets are searched to determine the typical February. As is usually the case, the typical January and the typical February may not be from the same year. Typical months are determined for the remaining months and some data ‘smoothing’ done for the transition between months. An hour-by-hour data base is then generated of readings for all recorded weather parameters from each of the ‘typical’ months and is called a typical meteorological year.
A recent set of typical meteorological year data sets for the United States, called TMY2 data sets, has been derived from the 30-year historical National Solar Radiation Data Base. This database consists of hourly values, from 239 sites, of global and direct solar irradiance and numerous associated weather parameters from the years 1961 to 1990. These data, along with a user’s manual describing the derivation and format of the data may be found at the NREL internet site: User's Manual for TMY2s.
2.4.2 Clearness Index
Often, solar radiation levels are plotted in order to gain insight into the local and to permit extrapolation between sites where accurate databases exist. Examples of these are available on the NREL solar energy data site (see References at the end of this chapter). A concept used to normalize these maps, and to present location-specific solar radiation data is the clearness index,
(2.10)
where Ho,h may be found using Equation (2.4).
2.4.3 European and Worldwide Solar Radiation Data Bases
A solar radiation data base atlas has been developed under the auspices of the European Union (Scharmer & Greif, 2000). This atlas offers a unique instrument dedicated to the knowledge and exploitation of the solar resources for Europe in a broad sense, from Ural to Azores and from Northern Africa to Polar Circle and covers the period 1981-1990.
A computer program permitting calculation of hourly values of solar radiation data throughout the world is available and has been validated at many sites (METEONORM, 2000). The program is continually being updated to include more weather station data, reducing the amount of extrapolation necessary between sites.
2.4.4 Solar Radiation Atlases
Solar radiation
is defined as the amount of energy deposit ad at a specific location over a specific period of time. It is believed that solar radiation, averaged over a period of many days, is somewhat consistent within a distance scale of tens of miles over uniform terrain. The assumption may then be made that monthly or yearly solar radiation measured at locations hundreds of miles apart, can be interpolated to give valid solar radiation levels at any location between the points. Although these assumptions are currently under study, it is generally considered that solar radiation maps can provide some valid information about the solar climate.A complete compilation of radiation and weather data contour maps depicting global, direct and diffuse solar radiation along with weather data for the United States are presented in the Solar Radiation Resource Atlas of the United States (SERI, 198l). These maps are constantly being updated, and most are currently available on the NREL solar data web site.
Annual average daily solar radiation maps for global horizontal and direct (beam) normal are shown in Figures 2.16 and 2.17, respectively. Note that the global horizontal values are typically lower than the direct normal values as a result of the cosine effect on a horizontal surface discussed previously.
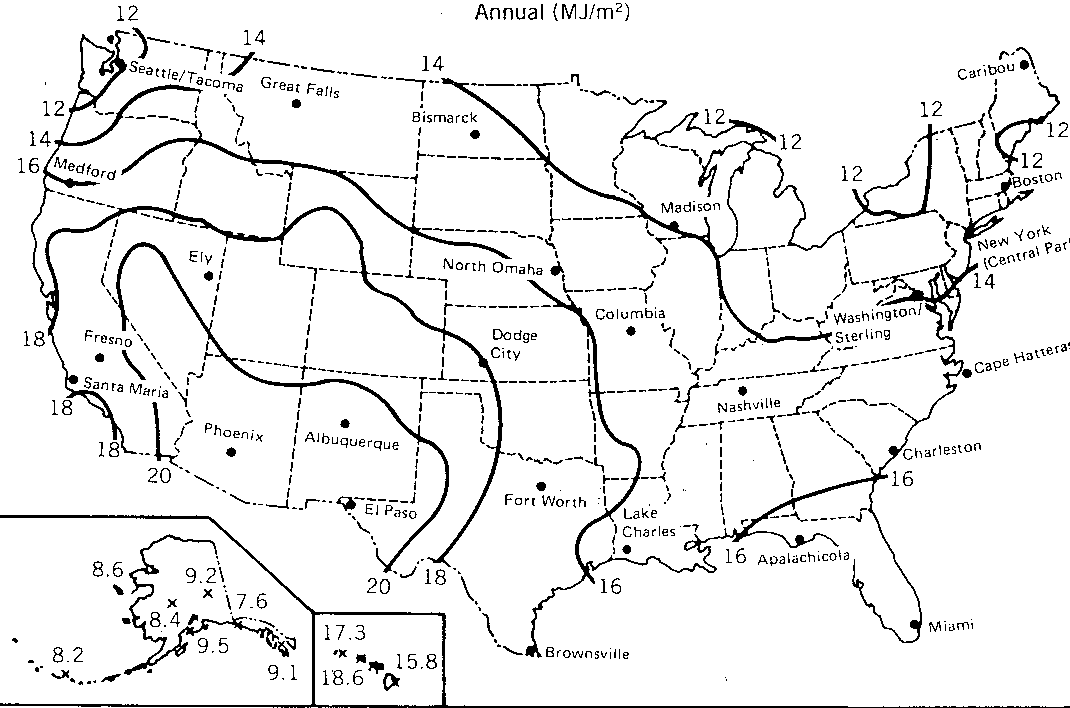
Figure 2.16
Annual average daily global horizontal solar radiation in the United States. Values are in MJ/m2 (SERI, 1981)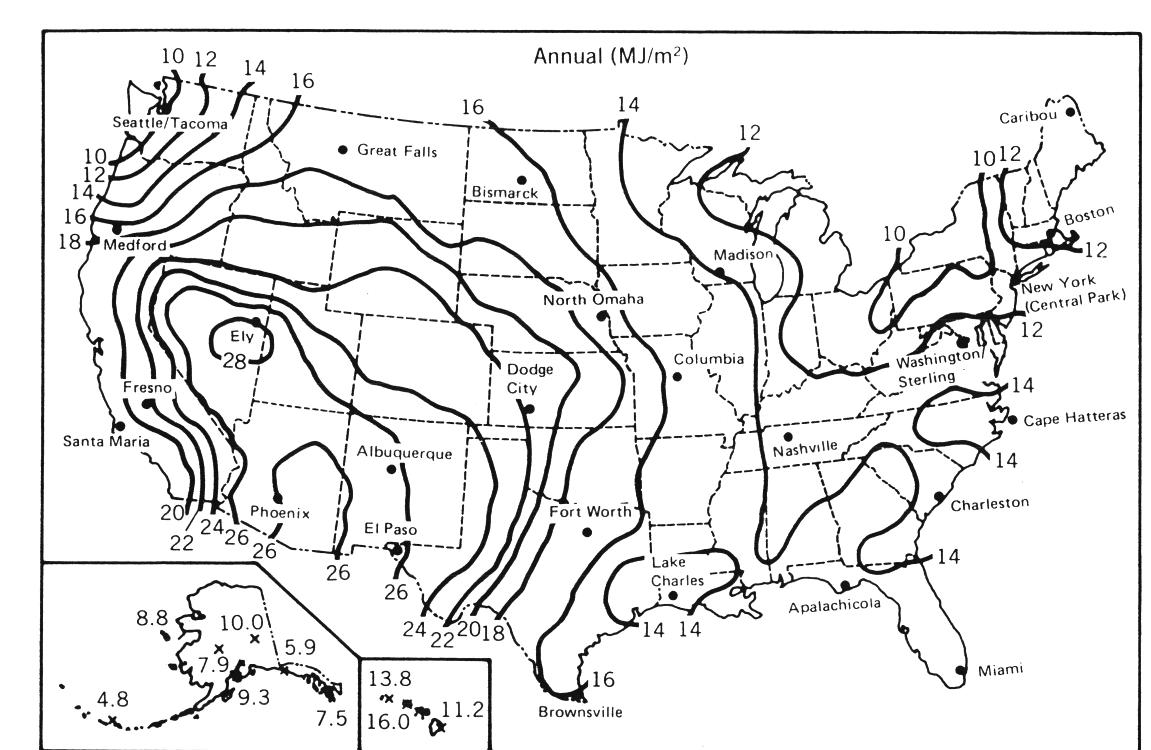
Solar atlas maps provide a graphic view of regional average solar radiation levels and are a quick source for finding monthly or yearly solar radiation levels. They are also useful in selecting the best TMY data set to use in determining the performance of a solar energy system located a considerable distance from any one of the TMY sites. To do this the designer selects the closest TMY site that has a similar average solar radiation.
One obvious warning in accepting the validity of solar radiation map data is the effect of microclimates. We all know of locations where fog will occlude the sun for a large portion of the day, and a few miles away it will be clear. Also, weather patterns tend to be affected on a micro-scale by mountainous terrain. The system designer should be aware of the existence of microclimates and their impact on system performance predicted by using any of these databases.
2.5 Analytical Models of Solar Irradiance
When developing a simple computer-based solar energy system performance model to study some aspect of system design, it is often unnecessary to include the massive data handling algorithms required to utilize data bases such as the TMY2 data base. An example would be doing sensitivity analyses of some component change within a solar energy conversion system. Closed-form solar irradiance models provide such a tool for inputting solar irradiance data into analytical models. However, the designer should be warned that the accuracy of any such model is extremely limited, and should only be used as a precursor to TMY or other hour-by-hour data solar energy databases.
2.5.1 A Simple Half-Sine Model
Often, a simple analytical model of clear-day solar irradiance is all that is needed to predict phenomena related to solar energy system design. One such model, used in the basic solar energy system model, SIMPLES described in Chapter 13, is the half-sine solar irradiance model. The only input required is the times of sunrise, sunset, and the peak, noontime solar irradiance level.
(2.11)
where t is the time in hours (24-hour clock), and the sine term is in degrees. Since this model produces negative values after sunset, a logical check for this in programs using this model must be implemented.
Example
: If sunrise is at 5:00, sunset at 19:00 and the noontime solar irradiance is 1,000 W/m2, this model predicts the solar irradiance at 9:00 as 782 W/m2.2.5.2 Hottel’s Clear-Day Model
The analysis of a solar energy system design is typically initiated by predicting its performance over a "typical" "clear" day. There are a number of clear-day mathematical solar irradiance models that may be used to predict the expected maximum hour-by-hour solar irradiance. An extensive discussion of various solar irradiance models may be found in Iqbal (1983). Since the system designer is encouraged to utilize solar irradiance databases rather than models for final analyses of system performance, only one model, a simple clear-day direct solar irradiance model by Hottel (1976), has been selected for presentation here.
Hottel’s clear-day model of direct normal solar irradiance is based on atmospheric transmittance calculations using the 1962 U.S. Standard Atmosphere as follows:
where
Io is the extraterrestrial irradiance, Equation (2.1) and
(2.13)
where
A is the local elevation in kilometers.For the urban 5-km (3.1-mi.) visibility haze model, the parameters are
(2.14)
The Hottel model may be extended to other climate types (consult the reference). For most purposes, however, only a standard atmosphere correlation will be useful.
If global horizontal solar irradiance is desired rather than direct normal, the diffuse irradiance component must also be approximated and then combined with the direct normal irradiance component described by Equation (2.9). A clear-day correlation of the diffuse component of solar radiation made by Liu and Jordan (1960) in terms of the atmospheric transmittance for direct radiation provides an expression for the diffuse radiation falling on a horizontal surface. Combined with Hottel’s direct normal model, the diffuse solar irradiance on a horizontal surface may be calculated as
where the terms are the same as described for Equation
(2.12). Other diffuse radiation models are discussed in Iqbal (1983). A comparison of the calculated results from Equations (2.12) and (2.15) are shown in Figure 2.18.Example
: Values of the direct and diffuse clear-day (23-km visibility) solar irradiance calculated by using Equations (2.12) and (2.15) for Albuquerque, NM (35.03 degrees latitude, 1.619 km elevation) on the summer solstice. These are shown in Figure 2.18 as solid lines in this figure. Also plotted are actual weather data for relatively clear days near the summer solstice from the Albuquerque typical meteorological year (TMY) weather database. Note that cloud cover lowers the direct and raises the diffuse radiation in the afternoon for three of the days. However, day 171 seems to be clear for the entire day.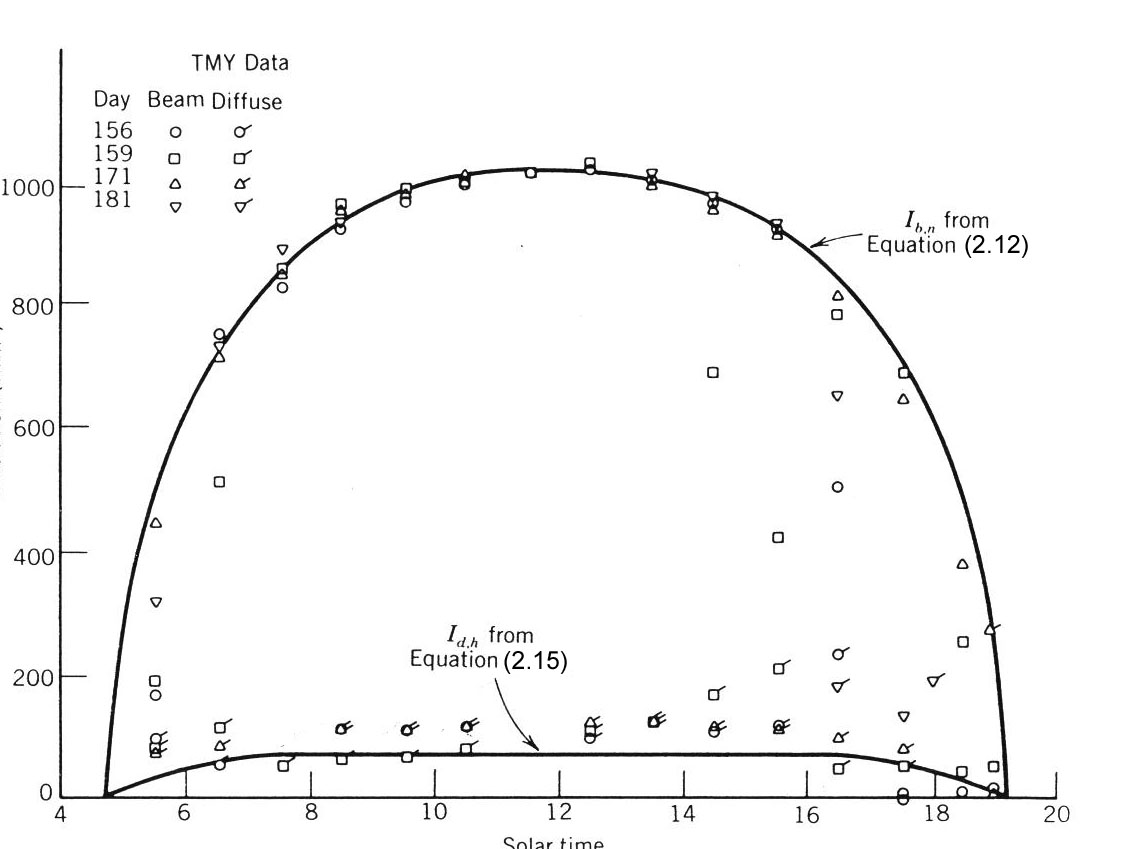
Figure 2.18 Comparison of Albuquerque TMY data with solar irradiance values predicted by clear-day direct and diffuse models for the same latitude and elevation on day 156.
Bibliography
Coulson, K. L. (1975), Solar and Terrestrial Radiation, Academic Press, New York.
Liou, K. N. (1980), An Introduction to Atmospheric Radiation, Academic Press, New York.
References
Bendt, P. and A. Rabl (1980), "Effect of Circumsolar Radiation on Performance of Focusing Collectors; "SERI Report TR-34 -093, April.
Bird, R. E., R. L. Hurlstrom, and J. L. Lewis (1983), "Terrestrial Solar Spectral Data Sets," Solar Energy 30(6), 563.
Boes, E. C. (1979a), "Fundamentals of Solar Radiation, "Sandia National Labs Report SAND79-0490, December.
Boes , E. C. (1979b), "Insolation Modeling Overview ," Energy 4, 523.
Cano, D., J.M. Monget, M. Albuisson, H. Guillard, N. Regas and L. Wald (1986), "A Method for the Determination of the Global Solar Radiation from Meteorological Satellite Data," Solar Energy, 37, pp 31-39.
Delinger, W. G. (1976), "The Definition of the Langley," Solar Energy, 18(4), 369.
Diak, G. R., C. Gautier, and S. Masse (1982),"An Operational System for Mapping Insolation from GOES Satellite Data," Solar Energy 28 (5), 371.
Duncan, C. H., R. C. Willson, J. M. Kendall, R. G. Harrison, and J. R. Hickey (1982), "Latest Rocket Measurements of the Solar Constant," Solar Energy 28 (5), 385.
Eddy, J. A. (1979), "A New Sun, the Solar Results from Skylab," NASA Report SP -402.
Fröhlich, C., and R. W. Brusa (1981), "Solar Radiation and its Variation in Time", Solar Physics 74, 209.
Hickey, J. R., B. M. Alton, F. J. Griffin, H. Jacobwitz, P. Pellegrino, R. H. Maschhoff, E. A. Smith, and T. H. Vonder Harr (1982), "Extraterrestrial Solar Irradiance Variability. Two and One-Half Years of Measurements from Nimbus 7," Solar Energy 29 (2), 125.
Hottel, H. C. (1976), "A Simple Model for Estimating the Transmittance of Direct Solar Radiation Through Clear Atmospheres," Solar Energy 18 (2), 129.
Ineichen, P. and R. Perez, "Derivation of Cloud Indel from Geostationary Satellites and Application to the Production of Solar Irradiance and Daylight Illuminance Data," Theoretical and Applied Climatology, February.
Iqbal, M. (1983), An Introduction to Solar Radiation, Academic Press, New York.
Kasten, F. and A. T. Young (1989),"Revised Optical Air Mass Tables and Approximation Formula" Applied Optics 28 (22), 4735-4738.
Knapp, C. L., T. L. Stoffel, and S. D. Whittaker (1980), "Insolation Data Manual," SERI Report SERI/SP-755-789, October.
Knapp, C. L. and T. L. Stoffel (1982), "Direct Normal Solar Radiation Data Manual, "SERI Report SERI/SP-281-1658, July.
Liu, B. Y. H., and R. C. Jordan (1960), "The Interrelationship and Characteristic Distribution of Direct, Diffuse and Total Solar Radiation," Solar Energy 4 (1).
METEONORM (2000), Meteonorm 2000 Version 4.0 - Global Meteorological Database, James & James (Science Publishers) London
Scharmer, K. and J. Greif (2000), "The European Solar Radiation Atlas, Vol. 1 : Fundamentals and maps and Vol 2: Data Base and Exploitation and Software, Les Presses de l'Ecole des Mines, Paris.
SERI (1981), "Solar Radiation Energy Resource Atlas of the United States," SERI Report SERI/SP-642-1037, October.
Thekaekara, M. P. (1976), "Solar Radiation Measurement: Techniques and Instrumentation," Solar Energy 18(4), 309.
Watt, A. D. (1978 ), "On the Nature and Distribution of Solar Radiation." U.S. Department of Energy Report HCP/T2552-01, March.
White, O. R. (Ed.) (1977), The Solar Output and Its Variation, Colorado Associated University Press Boulder, CO.
Internet Web Sites
http://rredc.nrel.gov/solar -- NREL's solar energy data site